题目内容
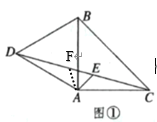
【题目】如图①,△ABC为等腰直角三角形, △ABD为等边三角形,连接CD.
(1)求∠ACD的度数;
(2)如图①,作∠BAC的平分线交CD于点E,求证:DE=AE+CE;
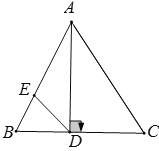
(3)如图②,在(2)的条件下,M为线段BC右侧一点,满足∠CMB=60°,求证:ME平分∠CMB.

【答案】(1)15°;(2)见解析;(3)见解析.
【解析】
(1)由题意可得∠BAC=90°,AB=AC,∠BAD=60°,AB=AD,于是可证得∠CAD=150°,AC=AD,故可求∠ACD的度数;
(2)在ED截取EF=AE,连接AF,证明△AEF为等边三角形,再证△ADF![]() △AEC,即可得出结论;
△AEC,即可得出结论;
(3)连接EB,作EG⊥BM于点G,EH⊥MC交MC的延长线于点H.证明△ABE![]() △AEC和△BEG
△AEC和△BEG![]() △HEC,于是可得EG=EH,根据角平分线的判定定理即可证明ME平分∠CMB.
△HEC,于是可得EG=EH,根据角平分线的判定定理即可证明ME平分∠CMB.
解:(1)如图①,
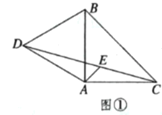
∵△ABC为等腰直角三角形,
∴∠BAC=90°,AB=AC,
∵△ABD为等边三角形,
∴∠BAD=60°,AB=AD,
∴∠CAD=150°,AC=AD,
∴∠ACD=![]() =15°,
=15°,
(2)在ED截取EF=AE,连接AF,
∵AE平分∠BAC,∠BAC=90°,
∴∠EAC=45°,
∵∠ACD=15°,
∴∠DEA=45°+15°=60°,
∵EF=AE,
∴△AEF为等边三角形,
∴AF=AE,∠FAE=60°,
∴∠FAD=150°-60°-45°=45°,
∴∠FAD=∠EAC,
在△ADF和△AEC中
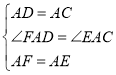 ,
,
∴△ADF![]() △AEC,
△AEC,
∴DF=CE,
∴DE=DF+EF=CE+AE,
(3)连接EB,作EG⊥BM于点G,EH⊥MC交MC的延长线于点H,
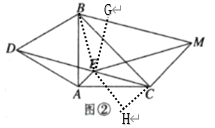
由(1)(2)可知在△ABE和△AEC中,
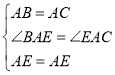
∴△ABE![]() △AEC,
△AEC,
∴BE=CE,∠AEB=∠AEC=120°,
∴∠BEC=360°-120°-120°=120°,
∵在四边形GEHM中,∠CMB=60°,EG⊥BM,EH⊥MC,
∴∠GEH=360°-60°-90°-90°=120°,
∴∠GEH=∠BEC,
∴∠CEH=∠BEG,
在△BEG和△HEC中,
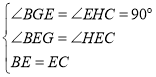
∴△BEG![]() △HEC,
△HEC,
∴EG=EH,
∴EM平分∠CMB.

【题目】在世界经济的影响下,国家采取扩大内需的政策,基建投资成为拉动内需最强有力的引擎,金强公司中标一项工程,在甲、乙两地施工,其中甲地需推土机30台,乙地需推土机26台,公司在A、B两地分别库存推土机32台和24台,现从A地运一台到甲、乙两地的费用分别是400元和300元.从B地运一台到甲、乙两地的费用分别为200元和500元,设从A地运往甲地x台推土机,运这批推土机的总费用为y元.
(1)根据题意,可将库存地和施工地之间推土机的运输数量列表如下:
甲地(台) | 乙地(台) | 合计 | |
A地 | x | A地库存:32 (台) | |
B地 | B地库存:24 (台) | ||
合计 | 甲地需求:30 (台) | 乙地需求:26 (台) | 总计:56 (台) |
(2)求y与x的函数关系式;
(3)当x取何值时,能使运送这批推土机的总费用最少?