题目内容
【题目】阅读与理解:
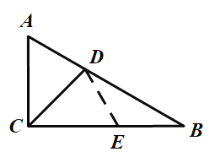
折纸,常常能为证明一个命题提供思路和方法.例如,在△ABC中,AB>AC(如图),怎样证明∠C>∠B呢?


把AC沿∠A的角平分线AD翻折,因为AB>AC,所以点C落在AB上的点![]() 处,即
处,即![]() ,据以上操作,易证明
,据以上操作,易证明![]() ≌
≌![]() ,所以
,所以![]() ,又因为
,又因为![]() >∠B,所以∠C>∠B.
>∠B,所以∠C>∠B.
感悟与应用:
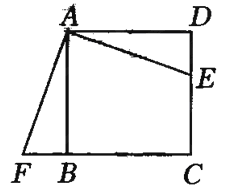
(1)如图(a),在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;
(2)如图(b),在四边形ABCD中,AC平分∠BAD,AC=16,AD=8,DC=BC=12,
① 求证:∠B+∠D=180°;
② 求AB的长.


【答案】(1)BC-AC=AD;(2)①见解析;②14;
【解析】
(1)在CB上截取CE=CA,连接DE.可证△ACD≌△ECD,得到DE=AD,∠A=∠CED=60°,进一步得到∠CED=2∠CBA,由外角的性质得到∠CBA=∠BDE,由等角对等边得到DE=BE,即可得到结论.
(2)①在AB上截取AE=AD,连接EC.易证△CDA≌△CEA,从而得到∠CEA=∠D,CE=CD.由等量代换得到BC=CE,由等边对等角得到∠B=∠CEB.再由邻补角的性质即可得到结论;
②过C作CF⊥AB于F.设FB=x,CF=h.由等腰三角形三线合一得到FE=BF=x.在Rt△BFC和Rt△FCA中,分别利用勾股定理列方程,求解即可.
(1)BC-AC=AD.理由如下:
如图,在CB上截取CE=CA,连接DE.
∵CD平分∠ACB,同理可证△ACD≌△ECD,∴DE=AD,∠A=∠CED=60°.
∵∠ACB=90°,∴∠CBA=30°,∴∠CED=2∠CBA.
∵∠CED=∠CBA+∠BDE,∴∠CBA=∠BDE,∴DE=BE,∴AD=BE.
∵BE=BC-CE=BC-AC,∴BC-AC=AD.
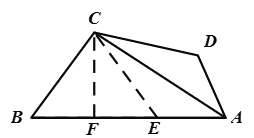
(2)①在AB上截取AE=AD,连接EC.
∵AC平分∠DAB,∴∠EAC=∠DAC.在△CDA和△CEA中,∵EA=DA,∠EAC=∠DAC,AC=AC,∴△CEA≌△CDA,∴∠CEA=∠D,CE=CD.
∵DC=BC,∴BC=CE,∴∠B=∠CEB.
∵∠CEA+∠CEB=180°,∴∠B+∠D=180°;
②过C作CF⊥AB于F.设FB=x,CF=h.
∵CB=CE,CF⊥BE,∴FE=BF=x.在Rt△BFC中,∵BF2+CF2=BC2,∴![]() ①;在Rt△FCA中,
①;在Rt△FCA中,![]() ②;解方程组①②得:x=3.∴AB=BF+FE+EA=2×3+8=14.
②;解方程组①②得:x=3.∴AB=BF+FE+EA=2×3+8=14.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案