题目内容
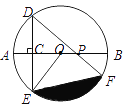
【题目】如下图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)∠A=∠GEF;(2)△BDF≌FEC.

【答案】(1)见解析;(2)见解析
【解析】
(1)由CD是⊙O的直径,所以∠DFC=∠ACB=90°,则DF∥AC,由平行线的性质可得∠A=∠BDF,再由圆周角定理得∠BDF=∠GEF,即可得∠A=∠GEF;
(2)连接DE,可证出四边形DECF是矩形,根据矩形的性质得DF=EC,EF=CD,再由直角三角形斜边上的中线得EF=CD=![]() AB=DB,根据HL即可得Rt△BDF≌Rt△FEC.
AB=DB,根据HL即可得Rt△BDF≌Rt△FEC.
证明:(1)∵CD是⊙O直径,
∴∠DFC=90°又∠ACB=90°,
∴DF∥AC,
∴∠A=∠BDF,
∵∠BDF=∠GEF(圆周角定理),
∴∠A=∠GEF;
(2)连接DE,
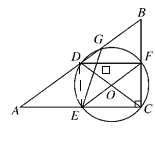
∵四边形DECF内接于⊙O,
∠ACB=90°,
∴∠EDF=∠DFC=∠ACB=90°,
∴四边形DECF是矩形,
∴DF=EC,EF=CD,又D是AB的中点,
∴EF=CD=![]() AB=DB,
AB=DB,
∴Rt△BDF≌Rt△FEC.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
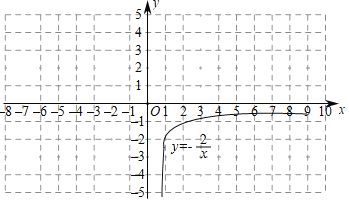
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2
﹣2![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.