题目内容
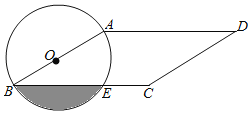
【题目】如图，在平行四边形ABCD中，AB＜AD，∠D=30°，CD=4，以AB为直径的⊙O交BC于点E，则阴影部分的面积为_____．
【答案】
【解析】
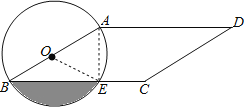
连接半径和弦AE，根据直径所对的圆周角是直角得：∠AEB=90°，继而可得AE和BE的长，所以图中弓形的面积为扇形OBE的面积与△OBE面积的差，因为OA=OB，所以△OBE的面积是△ABE面积的一半，可得结论．
如图，连接OE、AE，
∵AB是⊙O的直径，
∴∠AEB=90°，
∵四边形ABCD是平行四边形，
∴AB=CD=4，∠B=∠D=30°，
∴AE=
AB=2，BE=
=2
，
∵OA=OB=OE，
∴∠B=∠OEB=30°，
∴∠BOE=120°，
∴S阴影=S扇形OBE﹣S△BOE
=
=
，
故答案为：
．
练习册系列答案
相关题目
