Question

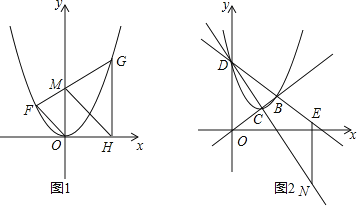
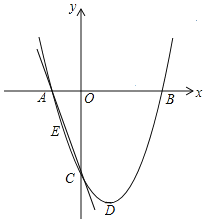
【题目】如图，抛物线y＝ax2﹣2ax+c的图象经过点C（0，﹣2），顶点D的坐标为（1，﹣），与x轴交于A、B两点．

（1）求抛物线的解析式；

（2）连接AC，E为直线AC上一点，当△AOC∽△AEB时，求点E的坐标和的值．

（3）点F （0，y）是y轴上一动点，当y为何值时，FC+BF的值最小．并求出这个最小值．

Answer 1

【答案】（1）y＝x2﹣x﹣2；（2）点E（﹣，﹣），＝；（3）﹣，．

【解析】

（1）将点C、D的坐标代入抛物线表达式，即可求解；

（2）当△AOC∽△AEB时，＝（）2＝（）2＝，求出yE＝﹣，由△AOC∽△AEB得：＝＝，即可求解；

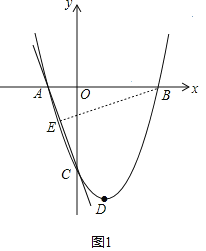
（3）如图2，连接BF，过点F作FG⊥AC于G，当折线段BFG与BE重合时，取得最小值，即可求解．

解：（1）由题可列方程组：，

解得：

∴抛物线解析式为：y＝x2﹣x﹣2；

（2）∵抛物线y＝x2﹣x﹣2的图象与x轴交于A、B两点，

∴点A（﹣1，0），点B（3，0），

∴AO＝1，BO＝3，

∴∠AOC＝90°，AC＝，AB＝4，

设直线AC的解析式为：y＝kx+b，

则，

解得：，

∴直线AC的解析式为：y＝﹣2x﹣2；

当△AOC∽△AEB时

∴＝（）2＝（）2＝，

∵S△AOC＝1，

∴S△AEB＝，

∴AB×|yE|＝，AB＝4，则yE＝﹣，

则点E（﹣，﹣）；

由△AOC∽△AEB得：＝＝，

∴＝；

（3）如图2，连接BF，过点F作FG⊥AC于G，

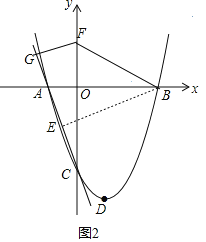
则FG＝CFsin∠FCG＝CF，

∴CF+BF＝GF+BF≥BE，

当折线段BFG与BE重合时，取得最小值，

由（2）可知∠ABE＝∠ACO

∴BE＝ABcos∠ABE＝ABcos∠ACO＝4×＝，

|y|＝OBtan∠ABE＝OBtan∠ACO＝3×＝，

∴当y＝﹣时，即点F（0，﹣），CF+BF有最小值为.