题目内容
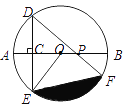
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
【答案】
【1】 根据垂径定理,得EC=![]()
弦DE垂直平分半径OA,![]()
由勾股定理,得出半径为2
【2】 连结OF
得出∠EOF=90°
得出![]()
【解析】
解:(1)∵直径AB⊥DE ∴![]()
∵DE平分AO ∴![]()
又∵![]() ∴
∴![]()
在Rt△COE中,![]()
∴⊙O的半径为2
(2)连结OF
在Rt△DCP中,∵![]() ∴
∴![]()
∴![]() ∵
∵![]()
∴S阴影=![]() 。。。。。。4
。。。。。。4
(1)因为AB⊥DE,求得CE的长,因为DE平分AO,求得CO的长,根据勾股定理求得⊙O的半径
(2)连结OF,根据S阴影=S扇形– S△EOF求得

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目