Question

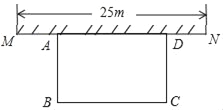
【题目】如图（1）所示，为矩形的边上一点，动点,同时从点出发，点沿折线运动到点时停止，点沿运动到点时停止，它们运动的速度都是秒，设、同时出发秒时，的面积为.已知与的函数关系图象如图（2）（曲线为抛物线的一部分）则下列结论正确的是（ ）

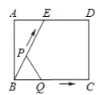
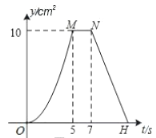
图（1） 图（2）

A.B.当是等边三角形时，秒

C.当时，秒D.当的面积为时，的值是或秒

Answer 1

【答案】D

【解析】

先根据图象信息求出AB、BE、BE、AE、ED，

A、直接求出比，

B、先判断出∠EBC≠60°，从而得出点P可能在ED上时，△PBQ是等边三角形，但必须是AD的中点，而AE＞ED，所以点P不可能到AD中点的位置，故△PBQ不可能是等边三角形；

C、利用相似三角形性质列出方程解决，分两种情况讨论计算即可，

D、分点P在BE上和点P在CD上两种情况计算即可．

由图象可知，AD＝BC＝BE＝5，CD＝AB＝4，AE＝3，DE＝2，

A、∴AB：AD＝5：4，故A错误，

B、∵tan∠ABE＝，

∴∠ABE≠30°

∴∠PBQ≠60°，

∴点P在ED时，有可能△PBQ是等边三角形，

∵BE＝BC，

∴点P到点E时，点Q到点C，

∴点P在线段AD中点时，有可能△PBQ是等边三角形，

∵AE＞DE，

∴点P不可能到AD的中点，

∴△PBQ不可能是等边三角形，故B错误，

C、∵△ABE∽△QBP，

∴点E只有在CD上，且满足，

∴，

∴CP＝．

∴t＝（BE＋ED＋DQ）÷1＝5＋2＋（4）＝．

故C错误，

D、①如图（1）

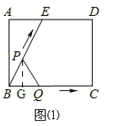
在Rt△ABE中，AB＝4，BE＝5

sin∠AEB＝，

∴sin∠CBE＝

∵BP＝t，

∴PG＝BPsin∠CBE＝t，

∴S△BPQ＝BQ×PG＝×t×t＝t2＝4，

∴t＝（舍）或t＝，

②当点P在CD上时，

S△BPQ＝×BC×PC＝×5×（5＋2＋4t）＝×（11t）＝4，

∴t＝，

∴当△BPQ的面积为4cm2时，t的值是或秒，故D正确，

故选：D．