题目内容
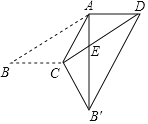
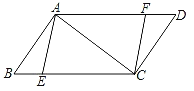
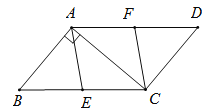
【题目】如图,在ABCD中,BC=10,对角线AC⊥AB,点EF在BC、AD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)当四边形AECF是菱形时,求BE的长.
【答案】(1)证明见解析;(2)5.
【解析】
(1)首先根据平行四边形的性质可得AD∥BC,AD=BC,再证明AF=EC,可证明四边形AECF是平行四边形;
(2)由菱形的性质得出AE=CE,得出∠EAC=∠ECA,由角的互余关系证出∠B=∠BAE,得出AE=BE,从而可得E为BC中点,即BE=![]() BC.
BC.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2)解:如图,∵四边形AECF是菱形,
∴AE=CE,
∴∠EAC=∠ECA,
∵AC⊥AB,
∴∠BAC=90°,
∴∠B+∠ECA=90°,∠BAE+∠EAC=90°,
∴∠B=∠BAE,
∴AE=BE,
∴BE=CE=![]() BC=
BC=![]() 10=5.
10=5.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目