题目内容
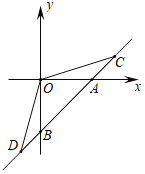
【题目】如图,直线l:y=x﹣2分别交x,y轴于A、B两点,C、D是直线l上的两个动点,点C在第一象限,点D在第三象限.且始终有∠COD=135°.
(1)求证:△OAC∽△DBO;
(2)若点C、D都在反比例函数y=![]() 的图象上,求k的值;
的图象上,求k的值;
(3)记△OBD的面积为S1,△AOC的面积为S2,且![]() =
=![]() ,二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当S1
,二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当S1![]() x
x![]() S2时,y有最大值2,求a的值.
S2时,y有最大值2,求a的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先求出点A,点B坐标,可求∠OAB=∠OBA=45°,由外角的性质可求∠DOB=∠ACO,∠AOC=∠ODB,可证△OAC∽△DBO;
(2)由相似三角形的性质可得![]() ,设
,设![]() =a>0,用a表示点C,点D坐标,代入反比例函数解析式,可求解;
=a>0,用a表示点C,点D坐标,代入反比例函数解析式,可求解;
(3)先求出点C,点D坐标,代入解析式,由题意可得当x=2时,y有最大值2,组成方程组,可求a的值.
解:(1)∵直线l:y=x﹣2分别交x,y轴于A、B两点,
∴点A(2,0),点B(0,﹣2),
∴AO=BO=2,
∴∠OAB=∠OBA=45°,
∴∠OCA+∠AOC=45°,∠ODB+∠DOB=45°,
∵∠COD=135°,
∴∠DOB+∠AOB+∠AOC=135°,
∴∠DOB+∠AOC=45°,
∴∠DOB=∠ACO,∠AOC=∠ODB,
∴△OAC∽△DBO;
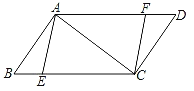
(2)如图,过点C作CF⊥x轴于F,过点D作DE⊥y轴于E,
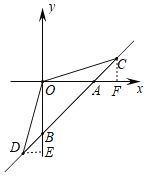
∵△OAC∽△DBO,
∴![]() ,
,
∴设![]() =a>0,
=a>0,
∴BD=![]() ,AC=2a,
,AC=2a,
∵∠CAF=∠OAB=45°,
∴∠ACF=∠CAF=45°,
∴AF=CF=![]() =
=![]() a,
a,
∴点C坐标(2+![]() a,
a,![]() a),
a),
同理可求点D坐标(﹣![]() ,﹣2﹣
,﹣2﹣![]() ),
),
∵点C、D都在反比例函数y=![]() 的图象上,
的图象上,
∴(2+![]() a)
a)![]() a=
a=![]() (2+
(2+![]() )
)
∴(![]() a2+2a+
a2+2a+![]() )(a+1)(a﹣1)=0,
)(a+1)(a﹣1)=0,
∵a>0,
∴![]() a2+2a+
a2+2a+![]() ≠0,a+1≠0,
≠0,a+1≠0,
∴a﹣1=0,
∴点C(2+![]() ,
,![]() )
)
∴k=![]() (2+
(2+![]() )=
)=![]() ;
;
(3)∵△OAC∽△DBO,
∴![]() ,
,
∴![]() ,
,
∴AC=2![]() ,
,
∴AF=CF=2,
∴点C(4,2),
∵![]() ,
,
∴![]() ,
,
∴BD=![]() ,
,
∴DE=BE=1,
∴点D(﹣1,﹣3),
∴△OBD的面积为S1=![]() ×2×1=1,△AOC的面积为S2=
×2×1=1,△AOC的面积为S2=![]() ×2×2=2,
×2×2=2,
∵二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当1≤x≤2时,y有最大值2,
∴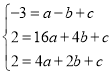 ,
,
解得: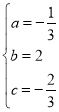 ,
,
∴a=![]() .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案【题目】为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机抽取40名学生进行问卷调查,其统计结果如表:
最喜欢的线上学习方式(每人最多选一种) | 人数 |
直播 | 10 |
录播 | a |
资源包 | 5 |
线上答疑 | 8 |
合计 | 40 |
(1)a= ;
(2)若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图,求“直播”对应扇形的圆心角度数;
(3)根据调查结果估计该校1000名学生中,最喜欢“线上答疑”的学生人数;
(4)在最喜欢“资源包”的学生中,有2名男生,3名女生.现从这5名学生中随机抽取2名学生介绍学习经验,求恰好抽到1名男生和1名女生的概率.