题目内容
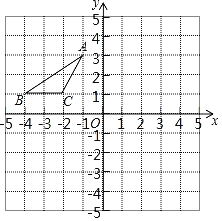
【题目】如图，在平行四边形ABCD中，∠B＝30°，且BC＝CA，将△ABC沿AC翻折至△AB′C，AB′交CD于点E，连接B′D．若AB＝3
，则B′D的长度为______．
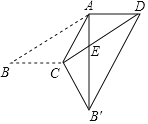
【答案】6
【解析】
作CM⊥AB于M，由折叠的性质得：B'C=BC=AC，∠AB'C=∠B=∠CAB'=30°，AB'=AB=CD，由平行四边形的性质得出AD=CB，AB=CD，∠ADC=∠B=30°，求出AD=AC，
，∠BAC=∠B=30°，由等腰三角形的性质得出∠ACD=∠ADC=30°，由直角三角形的性质得出
，证出AD=BC=2CM=3，再由勾股定理即可得出结果．
解：作CM⊥AB于M，如图所示：
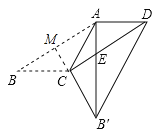
由折叠的性质得：B'C=BC=AC，∠AB'C=∠B=∠CAB'=30°，AB'=AB=CD，
∵四边形ABCD是平行四边形，
∴AD=CB，AB=CD，∠ADC=∠B=30°，∠BAD=∠BCD=180°-∠B=150°，
∴∠B'AD=150°-30°-30°=90°，
∵BC=AC，
∴，∠BAC=∠B=30°，
∴，
∴AD=BC=2CM=3，
在Rt△AB'D中，由勾股定理得：B'D=
；
故答案为：6．
练习册系列答案
相关题目
