题目内容
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
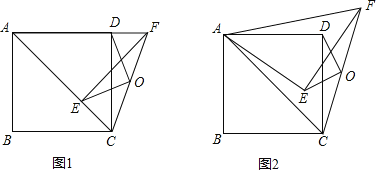
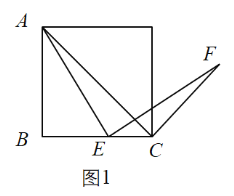
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
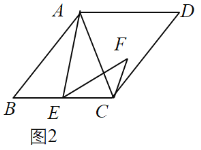
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
【答案】(1)![]() ,
,![]() ,理由见解析;(2)当
,理由见解析;(2)当![]() 时,(1)中的结论成立,理由见解析;(3)点O经过的路径长为
时,(1)中的结论成立,理由见解析;(3)点O经过的路径长为![]() .
.
【解析】
(1)根据直角三角形斜边上的中线等于斜边一半的性质可得OD与OE的数量关系;根据旋转的性质和正方形的性质可得AC=AF以及△ACF各内角的度数,进一步即可求出∠COE与∠DOF的度数,进而可得OD与OE的位置关系;
(2)延长EO到点M,使![]() ,连接DM、CM、DE,如图2所示,先根据SAS证明
,连接DM、CM、DE,如图2所示,先根据SAS证明![]() ≌
≌![]() ,得
,得![]() ,
,![]() ,再根据正方形的性质和旋转的性质推得
,再根据正方形的性质和旋转的性质推得![]() ,进一步在△ACF中根据三角形内角和定理和正方形的性质得出
,进一步在△ACF中根据三角形内角和定理和正方形的性质得出![]() ,再一次运用SAS推出
,再一次运用SAS推出![]() ≌
≌![]() ,于是
,于是![]() ,进一步即可得出OE、OD的位置关系,然后再运用SAS推出
,进一步即可得出OE、OD的位置关系,然后再运用SAS推出![]() ≌
≌![]() ,即可得OD与OE的数量关系;
,即可得OD与OE的数量关系;
(3)连接AO,如图3所示,先根据等腰三角形三线合一的性质得出![]() ,即可判断点O的运动路径,由
,即可判断点O的运动路径,由![]() 可得点O经过的路径长,进一步即可求得结果.
可得点O经过的路径长,进一步即可求得结果.
解:(1)![]() ,
,![]() ;理由如下:
;理由如下:
由旋转的性质得:![]() ,
,![]() ,
,
∵四边形ABCD是正方形,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,O为CF的中点,∴
,O为CF的中点,∴![]() ,
,
同理:![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ;
;
(2)当![]() 时,(1)中的结论成立,理由如下:
时,(1)中的结论成立,理由如下:
延长EO到点M,使![]() ,连接DM、CM、DE,如图2所示:
,连接DM、CM、DE,如图2所示:
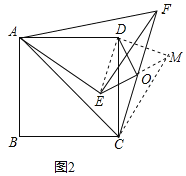
∵O为CF的中点,∴![]() ,
,
在![]() 和
和![]() 中,
中,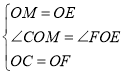 ,
,
∴![]() ≌
≌![]() (SAS),∴
(SAS),∴![]() ,
,![]() .
.
∵四边形ABCD是正方形,∴![]() ,
,![]() ,
,
∵![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,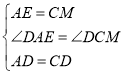 ,
,
∴![]() ≌
≌![]() (SAS),∴
(SAS),∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,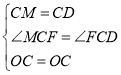 ,
,
∴![]() ≌
≌![]() (SAS),∴
(SAS),∴![]() .
.
∴![]() ,∴
,∴![]() ,
,![]() ;
;
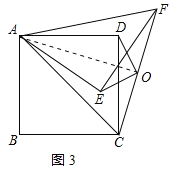
(3)连接AO,如图3所示:
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴点O在以AC为直径的圆上运动,
∵![]() ,∴点O经过的路径长等于以AC为直径的圆的周长,
,∴点O经过的路径长等于以AC为直径的圆的周长,
∵![]() ,∴点O经过的路径长为:
,∴点O经过的路径长为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案