��Ŀ����
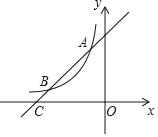
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������ֱ�ΪA����3��3����B����5��2����C����1��1����
��1���Ե�CΪλ�����ģ�������ABC��λ��ͼ�Ρ�A1B1C��ʹ��λ�Ʊ�Ϊ1��2����ABCλ�ڵ�C����࣬����ʾ����A1�����꣮
��2��������ABC�Ƶ�C˳ʱ����ת90�����ͼ�Ρ�A2B2C��
��3���ڣ�2���������������B������·�������������������

���𰸡���1����������A1(3����3)����2������������3��![]()
��������
��1���ӳ�BC��B1��ʹB1C=2BC���ӳ�AC��A1��ʹA1C=2AC����˳�����Ӽ��ɵá�A1B1C����д��A1���꼴�ɣ�
��2���ֱ�����A��B��C��˳ʱ����ת90����Ķ�Ӧ��A2��B2����˳�����Ӽ��ɵá�A2B2C��
��3����B���˶�·��Ϊ��CΪԲ�ģ�Բ�Ľ�Ϊ90���Ļ��������û�����ʽ������⣮
�⣺��1����ͼ����A1B1CΪ��������A1������Ϊ��3����3����
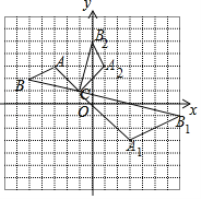
��2����ͼ����A2B2CΪ������
��3��CB=![]() ��
��
���Ե�B������·����=![]() ����
����

��ϰ��ϵ�д�
 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
�����Ŀ