题目内容
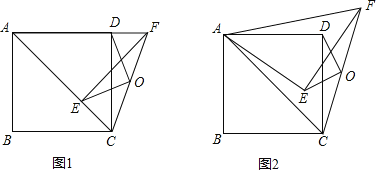
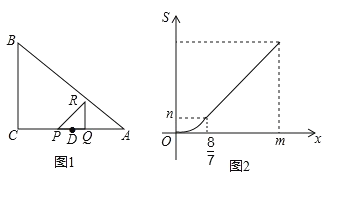
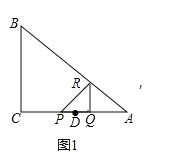
【题目】如图1,在△ABC中,∠C=90°,点D在AC上,且CD>DA,DA=2.点P、Q同时从D点出发,以相同的速度分别沿射线DC、射线DA运动.过点Q作AC的垂线段QR,使QR=PQ,联接PR.当点Q到达A时,点P、Q同时停止运动.设PQ=x.△PQR和△ABC重合部分的面积为S.S关于x的函数图像如图2所示(其中0<x≤![]() ,
,![]() <x≤m时,函数的解析式不同)
<x≤m时,函数的解析式不同)
(1)填空:n的值为___________;
(2)求S关于x的函数关系式,并写出x的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
【解析】
(1)当x=![]() 时,△PQR和△ABC重合部分的面积为S就是△PQR的面积;
时,△PQR和△ABC重合部分的面积为S就是△PQR的面积;
(2)分0<x≤![]() ,
,![]() <x≤m两种情况讨论即可;
<x≤m两种情况讨论即可;
(1)如图1,
当x=![]() 时,△PQR和△ABC重合部分的面积为S就是△PQR的面积
时,△PQR和△ABC重合部分的面积为S就是△PQR的面积
此时,S=![]() ×
×![]() ×
×![]() =
=![]() ,所以n=
,所以n=![]() .
.
(2)如图2

根据S关于x的函数图象,可得S关于x的函数表达式有两种情况:
当0<x≤![]() 时,S=
时,S=![]() ×PQ×RQ=
×PQ×RQ=![]()
![]() ,
,
Q点运动到A时,x=2AD=4,所以m=4.
当![]() <x≤4时,
<x≤4时,![]() ,
,
![]()
![]() △AQE∽△AQ1R1,
△AQE∽△AQ1R1,![]() ,
,
![]() QE=
QE=![]()
设FG=PG=a,
![]() △AGF∽△AQ1R1,
△AGF∽△AQ1R1,![]() ,
,
![]() AG=2+
AG=2+![]() -a,
-a,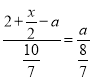 ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
综上,可得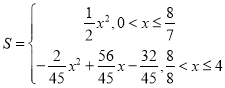

 寒假学与练系列答案
寒假学与练系列答案【题目】某医药研究所研发了一种新药,试验药效时发现:1.5小时内,血液中含药量y(微克)与时间x(小时)的关系可近似地用二次函数y=ax2+bx表示;1.5小时后(包括1.5小时),y与x可近似地用反比例函数y=![]() (k>0)表示,部分实验数据如表:
(k>0)表示,部分实验数据如表:
时间x(小时) | 0.2 | 1 | 1.8 | … |
含药量y(微克) | 7.2 | 20 | 12.5 | … |
(1)求a、b及k的值;
(2)服药后几小时血液中的含药量达到最大值?最大值为多少?
(3)如果每毫升血液中含药量不少于10微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间.(![]() ≈1.41,精确到0.1小时)
≈1.41,精确到0.1小时)