Question

【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法，下面是对一道几何题进行变式探究的思路，请你运用上述思想方法完成探究任务．

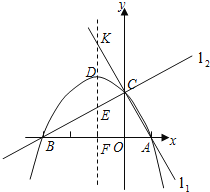
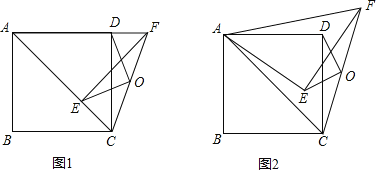
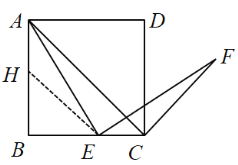
问题情境：在四边形中，是对角线，为边上一点，连接.以为旋转中心，将线段顺时针旋转，旋转角与相等，得到线段，连接．

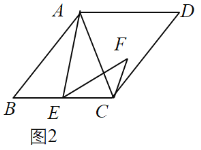
（1）特例如图1，若四边形是正方形，则与位置关系是_________．此时可以过点作的平行线来对结论进行证明（这里不要求证明）

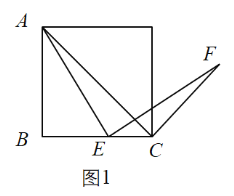
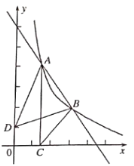
（2）拓展探究：如图2，若四边形是菱形，当时，求的度数；

Answer 1

【答案】（1）；（2）50°．

【解析】

（1）如图1中，作EH∥AC交AB于H．只要证明△HAE≌△CEF，即可推出∠AHE=∠ECF=135°，由∠BCA=45°，推出∠ACF=90°；

（2）如图2中，作EH∥AC交AB于H．只要证明△HAE≌△CEF，即可解决问题．

解：（1）证明：如图1中，作EH∥AC交AB于H．

∵四边形ABCD是正方形，

∴AB=BC，∠BAC=∠BCA=45°，

∵EH∥AC，

∴∠BHE=∠BAC=45°，∠BEH=∠BCA=45°，

∴∠BHE=∠BEH=45°，∠AHE=135°，

∴BH=BE， ∴AH=CE，

∵∠AEC=∠B+∠BAE=∠AEF+∠CEF，

∵∠AEF=∠B=90°，

∴∠HAE=∠CEF，

在△HAE和△CEF中，

∴△HAE≌△CEF，

∴∠AHE=∠ECF=135°，

∵∠BCA=45°，

∴∠ACF=90°，

∴AC⊥CF．

故答案为：AC⊥CF.

（2）如图2中，过点E作EH∥AC交AB于H.

∵四边形ABCD是菱形，

∴AB＝BC，∠BAC＝∠BCA，

∵EH∥AC，

∴∠BHE＝∠BAC，∠BEH＝∠BCA，

∴∠BHE＝∠BEH，

∴BH＝BE，

∴AH＝CE，

∵∠AEC＝∠B+∠BAE＝∠AEF+∠CEF，

∵∠AEF＝∠B，

∴∠HAE＝∠CEF，

在△HAE和△CEF中，

，

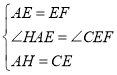∴△HAE≌△CEF，

∴∠AHE＝∠ECF，

∵∠B＝50°，

∴∠BHE＝∠ACB＝65°，

∴∠AHE＝∠ECF＝115°

∴∠ACF＝115°﹣65°＝50°.