Question

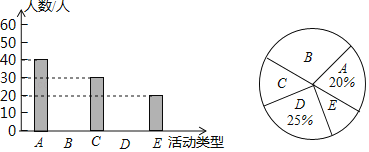
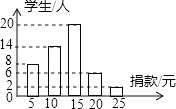
【题目】在慈善一日捐活动中，学校团总支为了了解本校学生的捐款情况，随机抽取了50名学生的捐款数进行了统计，并绘制成下面的统计图，

（1）这50名同学捐款的众数为　 　元，中位数为　 　元；

（2）求这50名同学捐款的平均数；

（3）该校共有800名学生参与捐款，请估计该校学生的捐款总数．

Answer 1

【答案】（1）15，15；（2）13；（3）10400

【解析】

（1）根据众数的定义即出现次数最多的数据进而得出即可，再利用中位数的定义得出即可；

（2）利用条形统计图得出各组频数，再根据加权平均数的公式计算即可；

（3）利用样本估计总体的思想，用总数乘以捐款平均数即可得到捐款总数．

解：（1）数据15元出现了20次，出现次数最多，所以众数是15元；

数据总数为50，所以中位数是第25、26位数的平均数，即（15+15）÷2＝15（元）．

故答案为15，15；

（2）50名同学捐款的平均数＝（5×8+10×14+15×20+20×6+25×2）÷50＝13（元）；

（3）估计这个中学的捐款总数＝800×13＝10400（元）．