题目内容
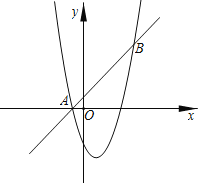
【题目】如图,抛物线解析式为y=x2,点A1的坐标为(1,1),连接OA1;过A1作A1B1⊥OA1,分别交y轴、抛物线于点P1、B1;过B1作B1A2⊥A1B1分别交y轴、抛物线于点P2、A2;过A2作A2B2⊥B1A2,分别交y轴、抛物线于点P3、B2…;则点Pn的坐标是_____.
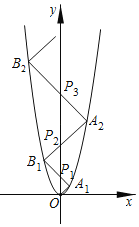
【答案】(0,n2+n)
【解析】
根据待定系数法分别求得直线OA1、A2B1、A2B2……的解析式,即可求得P1、P2、P3…的坐标,得出规律,从而求得点Pn的坐标.
解:∵点A1的坐标为(1,1),
∴直线OA1的解析式为y=x,
∵A1B1⊥OA1,
∴OP1=2,
∴P1(0,2),
设A1P1的解析式为y=kx+b1,
∴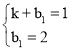 ,解得
,解得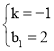 ,
,
∴直线A1P1的解析式为y=﹣x+2,
解![]() 求得B1(﹣2,4),
求得B1(﹣2,4),
∵A2B1∥OA1,
设B1P2的解析式为y=x+b2,
∴﹣2+b2=4,
∴b2=6,
∴P2(0,6),
解![]() 求得A2(3,9)
求得A2(3,9)
设A1B2的解析式为y=﹣x+b3,
∴﹣3+b3=9,
∴b3=12,
∴P3(0,12),
…
∴Pn(0,n2+n),
故答案为(0,n2+n).

练习册系列答案
相关题目
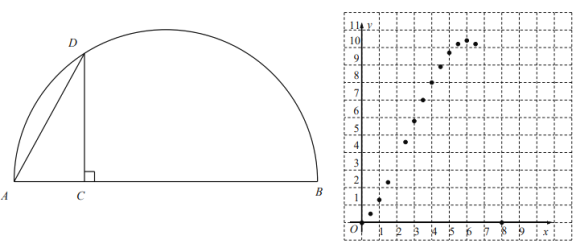
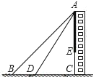
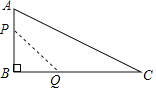
【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.