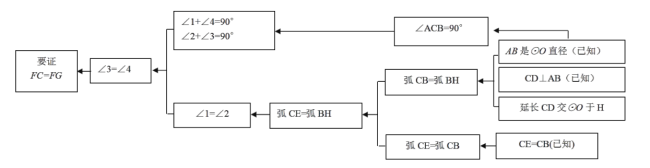
题目内容
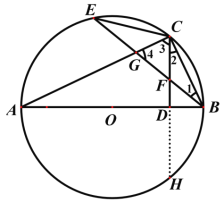
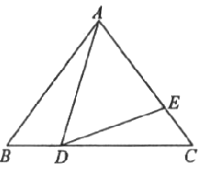
【题目】如图1,△ABC~△ADE,∠BAC=∠DAE=90°,AB=6,AC=8,点D在线段BC上运动,
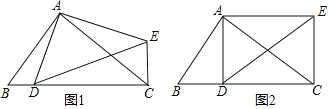
(1)如图1,求证:△ABD∽△ACE
(2)如图2,当AD⊥BC时,判断四边形ADCE的形状,并证明.
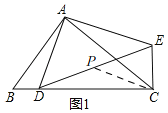
(3)当点D从点B运动到点C时,设P为线段DE的中点,在点D的运动过程中,求CP的最小值.
【答案】(1)见解析;(2)四边形ADCE是矩形,见解析;(3)4
【解析】
(1)先判断出∠BAD=∠CAE,再判断出![]() ,即可得出结论;
,即可得出结论;
(2)先判断出∠ADB=90°,根据相似判断出∠AEC=90°,即可得出结论;
(3)先判断出CP最小时,AD最小,再根据直角三角形的面积的计算方法求出AD的最小值,即可得出结论.
解:(1)∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵△ABC~△ADE,
∴![]() ,
,
∴△ABD∽△ACE;
(2)∵AD⊥BC,
∴∠ADC=∠ADB=90°,
由(1)知△ABD∽△ACE,
∴∠AEC=∠ADB=90°,
∵∠DAE=90°,
∴∠ADC=∠DAE=∠AEC=90°,
∴四边形ADCE是矩形;
(3)如图1,
连接CP,
在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,
∵△ABC∽△ADE,
∴![]() ,
,
∴DE=![]() =
=![]() AD=
AD=![]() AD,
AD,
由(1)知,△ABD∽△ACE,
∴∠ABD=∠ACE,
∵∠BAC=90°,
∴∠ABD+∠ACB=90°,
∴∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=90°,
∴CP=![]() DE,
DE,
∵DE=![]() AD,
AD,
∴CP=![]() ×
×![]() AD=
AD=![]() AD,
AD,
要CP最小,则AD最小,
即:当AD⊥BC时,AD最小,
∵S△ABC=![]() ABAC=
ABAC=![]() BCAD最小,
BCAD最小,
∴AD最小=![]() ,
,
即:CP最小=![]() AD最小=
AD最小=![]() ×
×![]() =4,
=4,
即CP的最小值为4.

【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
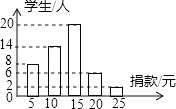
a.七年级成绩频数分布直方图:
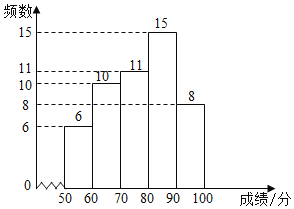
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.