ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΫϋΤΎ÷μ»βΦέΗώ≤ΜΕœΉΏΗΏΘ§“ΐΤπΝΥΟώ÷Ύ”κ’ΰΗ°ΒΡΗΏΕ»ΙΊΉΔΘ§Β± –≥Γ÷μ»βΒΡΤΫΨυΦέΗώΟΩ«ßΩΥ¥οΒΫ“ΜΕ®ΒΡΒΞΦέ ±Θ§’ΰΗ°ΫΪΆΕ»κ¥Δ±Η÷μ»β“‘ΤΫ“÷÷μ»βΦέΗώΘ°ΨίΆ≥ΦΤΘΚ¥”ΫώΡξΡξ≥θ÷Ν7‘¬20»’Θ§÷μ»βΦέΗώ≤ΜΕœΉΏΗΏΘ§7‘¬20»’±»Ρξ≥θΦέΗώ…œ’«ΝΥ60%Θ°Ρ≥ –Οώ”ΎΡ≥≥§ –ΫώΡξ7‘¬20»’ΙΚ¬ρ2.5«ßΩΥ÷μ»βΜ®100‘Σ«°Θ°
Θ®1Θ©Έ ΘΚΡ«Ο¥ΫώΡξΡξ≥θ÷μ»βΒΡΦέΗώΈΣΟΩ«ßΩΥΕύ…Ό‘ΣΘΩ
Θ®2Θ©Ρ≥≥§ –ΫΪΫχΜθΦέΈΣΟΩ«ßΩΥ30‘ΣΒΡ÷μ»βΘ§Α¥7‘¬20»’ΦέΗώ≥ω έΘ§ΤΫΨυ“ΜΧλΡήœζ έ≥ω100«ßΩΥΘ§Ψ≠Βς≤ι±μΟςΘΚ÷μ»βΒΡ έΦέΟΩ«ßΩΥœ¬ΫΒ1‘ΣΘ§Τδ»’œζ έΝΩΨΆ‘ωΦ”20«ßΩΥΘ§≥§ –ΈΣΝΥ Βœ÷œζ έ÷μ»βΟΩΧλ”–1120‘ΣΒΡœζ έάϊ»σΘ§ΈΣΝΥΨΓΩ…Ρή»ΟΙΥΩΆ”≈Μί”ΠΗΟΟΩ«ßΩΥΕ®ΦέΈΣΕύ…Ό‘ΣΘΩ
Θ®3Θ©7‘¬21»’Θ§Ρ≥ –ΨωΕ®ΆΕ»κ¥Δ±Η÷μ»β≤ΔΙφΕ®Τδ‘Ύ‘≠œζ έΦέΒΡΜυ¥Γ…œœ¬Βςa%≥ω έΘ§Ρ≥≥§ –Α¥ΙφΕ®Φέ≥ω έ“Μ≈ζ¥Δ±Η÷μ»βΘ§ΗΟ≥§ –‘ΎΖ«¥Δ±Η÷μ»βΒΡΦέΗώ≤Μ±δ«ιΩωœ¬Θ§ΗΟΧλΒΡΝΫ÷÷÷μ»βΉήœζΝΩ±»7‘¬20»’‘ωΦ”ΝΥa%Θ§«“¥Δ±Η÷μ»βΒΡœζΝΩ’ΦΉήœζΝΩΒΡ![]() Θ§ΝΫ÷÷÷μ»βœζ έΒΡΉήΫπΕν±»7‘¬20»’ΧαΗΏΝΥ
Θ§ΝΫ÷÷÷μ»βœζ έΒΡΉήΫπΕν±»7‘¬20»’ΧαΗΏΝΥ![]() a%Θ§«σaΒΡ÷ΒΘ°
a%Θ§«σaΒΡ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©25‘ΣΘΜΘ®2Θ©37‘ΣΘΜΘ®3Θ©aΒΡ÷ΒΈΣ20
ΓΨΫβΈωΓΩ
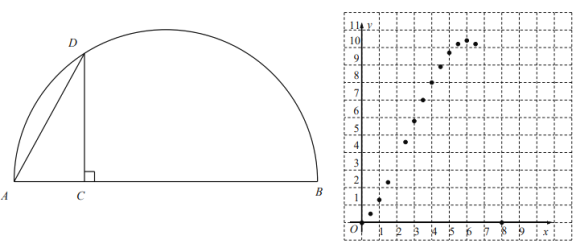
Θ®1Θ©άϊ”ΟΒΞΦέΘΫΉήΦέΓ¬ ΐΝΩΩ…«σ≥ω7‘¬20»’÷μ»βΒΡΒΞΦέΘ§…ηΫώΡξΡξ≥θ÷μ»βΒΡΦέΗώΈΣΟΩ«ßΩΥx‘ΣΘ§ΗυΨίΡξ≥θ”κ7‘¬20»’÷μ»βΒΞΦέΦδΒΡΙΊœΒΘ§Ω…ΒΟ≥ωΙΊ”ΎxΒΡ“Μ‘Σ“Μ¥ΈΖΫ≥ΧΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©…ηΟΩ«ßΩΥΫΒΦέy‘ΣΘ§‘ρ»’œζ έΘ®100+20yΘ©«ßΩΥΘ§ΗυΨίΉήάϊ»σΘΫΟΩ«ßΩΥΒΡάϊ»σΓΝœζ έ ΐΝΩΘ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎyΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωy÷ΒΘ§‘ΌΫΪΤδΫœ¥σ÷Β¥ζ»κΘ®40©¹yΘ©÷–Φ¥Ω…«σ≥ωΫα¬έΘΜ
Θ®3Θ©…ηΗΟ≥§ –7‘¬20»’ έ≥ωm«ßΩΥ÷μ»βΘ§ΗυΨίœζ έΉήΫπΕνΘΫœζ έΒΞΦέΓΝœζ έ ΐΝΩΘ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎaΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ§Ϋβ÷°»ΓΤδ’ΐ÷ΒΦ¥Ω…ΒΟ≥ωΫα¬έΘ°
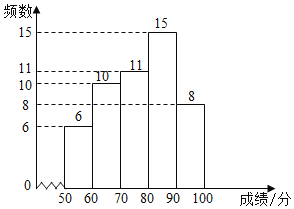
Θ®1Θ©ΫώΡξ7‘¬20»’÷μ»βΒΡΦέΗώΘΫ100Γ¬2.5ΘΫ40Θ®‘Σ/«ßΩΥΘ©Θ°
…ηΫώΡξΡξ≥θ÷μ»βΒΡΦέΗώΈΣΟΩ«ßΩΥx‘ΣΘ§
“άΧβ“βΘ§ΒΟΘΚΘ®1+60%Θ©xΘΫ40Θ§
ΫβΒΟΘΚxΘΫ25Θ°
¥πΘΚΫώΡξΡξ≥θ÷μ»βΒΡΦέΗώΈΣΟΩ«ßΩΥ25‘ΣΘ°
Θ®2Θ©…ηΟΩ«ßΩΥΫΒΦέy‘ΣΘ§‘ρ»’œζ έΘ®100+20yΘ©«ßΩΥΘ§
“άΧβ“βΘ§ΒΟΘΚΘ®40©¹30©¹yΘ©Θ®100+20yΘ©ΘΫ1120Θ§
’ϊάμΘ§ΒΟΘΚy1ΘΫ2Θ§y2ΘΫ3Θ§
ΓΏΨΓΩ…Ρή»ΟΙΥΩΆ”≈ΜίΘ§
ΓύyΘΫ3Θ§
Γύ40©¹yΘΫ37Θ°
¥πΘΚ”ΠΗΟΟΩ«ßΩΥΕ®ΦέΈΣ37‘ΣΘ°
Θ®3Θ©…ηΗΟ≥§ –7‘¬20»’ έ≥ωm«ßΩΥ÷μ»βΘ§
“άΧβ“βΘ§ΒΟΘΚ40Θ®1©¹a%Θ©ΓΝ![]() Θ®1+a%Θ©m+40ΓΝ
Θ®1+a%Θ©m+40ΓΝ![]() Θ®1+a%Θ©mΘΫΘ®1+
Θ®1+a%Θ©mΘΫΘ®1+![]() a%Θ©ΓΝ40mΘ§
a%Θ©ΓΝ40mΘ§
’ϊάμΘ§ΒΟΘΚa2©¹20aΘΫ0Θ§
ΫβΒΟΘΚa1ΘΫ0Θ®…α»ΞΘ©Θ§a2ΘΫ20Θ°
¥πΘΚaΒΡ÷ΒΈΣ20Θ°

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΫβΤΏΓΔΑΥΡξΦΕ―ß…ζΕ‘ΓΑΖάΡγΥ°Γ±Α≤»Ϊ÷Σ ΕΒΡ’ΤΈ’«ιΩωΘ§¥”ΤΏΓΔΑΥΡξΦΕΗςΥφΜζ≥ι»Γ50Οϊ―ß…ζΫχ––≤β ‘Θ§≤ΔΕ‘≥…Φ®Θ®ΑΌΖ÷÷ΤΘ©Ϋχ––’ϊάμΓΔΟη ωΚΆΖ÷ΈωΘ°≤ΩΖ÷–≈œΔ»γœ¬ΘΚ
aΘ°ΤΏΡξΦΕ≥…Φ®ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΚ
bΘ°ΤΏΡξΦΕ≥…Φ®‘Ύ![]() ’β“ΜΉιΒΡ «ΘΚ70 72 74 75 76 76 77 77 77 78 79
’β“ΜΉιΒΡ «ΘΚ70 72 74 75 76 76 77 77 77 78 79
cΘ°ΤΏΓΔΑΥΡξΦΕ≥…Φ®ΒΡΤΫΨυ ΐΓΔ÷–ΈΜ ΐ»γœ¬ΘΚ
ΡξΦΕ | ΤΫΨυ ΐ | ÷–ΈΜ ΐ |
ΤΏ | 76.9 | m |
ΑΥ | 79.2 | 79.5 |
ΗυΨί“‘…œ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
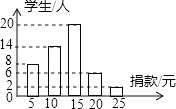
Θ®1Θ©‘Ύ’β¥Έ≤β ‘÷–Θ§ΤΏΡξΦΕ‘Ύ80Ζ÷“‘…œΘ®Κ§80Ζ÷Θ©ΒΡ”–ΓΓ ΓΓ»ΥΘΜ
Θ®2Θ©±μ÷–mΒΡ÷ΒΈΣΓΓ ΓΓΘΜ
Θ®3Θ©‘Ύ’β¥Έ≤β ‘÷–Θ§ΤΏΡξΦΕ―ß…ζΦΉ”κΑΥΡξΦΕ―ß…ζ““ΒΡ≥…Φ®ΕΦ «78Ζ÷Θ§«κ≈–ΕœΝΫΈΜ―ß…ζ‘ΎΗςΉ‘ΡξΦΕΒΡ≈≈ΟϊΥ≠ΗϋΩΩ«ΑΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®4Θ©ΗΟ–ΘΤΏΡξΦΕ―ß…ζ”–400»ΥΘ§ΦΌ…η»Ϊ≤Ω≤ΈΦ”¥Υ¥Έ≤β ‘Θ§«κΙάΦΤΤΏΡξΦΕ≥…Φ®≥§ΙΐΤΫΨυ ΐ76.9Ζ÷ΒΡ»Υ ΐΘ°
ΓΨΧβΡΩΓΩ»γΆΦΘ§![]() «œΏΕΈ
«œΏΕΈ![]() …œ--Ε·ΒψΘ§“‘
…œ--Ε·ΒψΘ§“‘![]() ΈΣ÷±ΨΕΉςΑκ‘≤Θ§ΙΐΒψ
ΈΣ÷±ΨΕΉςΑκ‘≤Θ§ΙΐΒψ![]() Ής
Ής![]() ΫΜΑκ‘≤”ΎΒψ
ΫΜΑκ‘≤”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() .“―÷Σ
.“―÷Σ![]() Θ§…η
Θ§…η![]() ΝΫΒψΦδΒΡΨύάκΈΣ
ΝΫΒψΦδΒΡΨύάκΈΣ![]() Θ§
Θ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() .(Β±Βψ
.(Β±Βψ![]() ”κΒψ
”κΒψ![]() ΜρΒψ
ΜρΒψ![]() ÷ΊΚœ ±Θ§
÷ΊΚœ ±Θ§![]() ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ![]() )«κΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐ
)«κΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐ![]() ΥφΉ‘±δΝΩ
ΥφΉ‘±δΝΩ![]() ΒΡ±δΜ·Εχ±δΜ·ΒΡΙφ¬…Ϋχ––ΧΫΨΩ. (ΉΔ: ±ΨΧβΥυ”– ΐ÷ΒΨυ±ΘΝτ“ΜΈΜ–Γ ΐ)
ΒΡ±δΜ·Εχ±δΜ·ΒΡΙφ¬…Ϋχ––ΧΫΨΩ. (ΉΔ: ±ΨΧβΥυ”– ΐ÷ΒΨυ±ΘΝτ“ΜΈΜ–Γ ΐ)
![]() Ά®ΙΐΜ≠ΆΦΓΔ≤βΝΩΓΔΦΤΥψΘ§ΒΟΒΫΝΥ
Ά®ΙΐΜ≠ΆΦΓΔ≤βΝΩΓΔΦΤΥψΘ§ΒΟΒΫΝΥ![]() ”κ
”κ![]() ΒΡΦΗΉι÷ΒΘ§»γœ¬±μ:
ΒΡΦΗΉι÷ΒΘ§»γœ¬±μ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤Ι»Ϊ±μΗώ÷–ΒΡ ΐ÷Β: ![]() ΘΜ
ΘΜ![]() ΘΜ
ΘΜ![]() .
.
![]() ΗυΨί±μ÷– ΐ÷ΒΘ§ΦΧ–χΟη≥ω
ΗυΨί±μ÷– ΐ÷ΒΘ§ΦΧ–χΟη≥ω![]() ÷– Θ”ύΒΡ»ΐΗωΒψ
÷– Θ”ύΒΡ»ΐΗωΒψ![]() Θ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσ≤Δ–¥≥ω’βΗωΚ· ΐΒΡ“ΜΧθ–‘÷ ;
Θ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσ≤Δ–¥≥ω’βΗωΚ· ΐΒΡ“ΜΧθ–‘÷ ;
![]() ΫαΚœΚ· ΐΆΦœσΘ§÷±Ϋ”–¥≥ωΒ±
ΫαΚœΚ· ΐΆΦœσΘ§÷±Ϋ”–¥≥ωΒ±![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() ±Θ§
±Θ§![]() ΒΡ≥ΛΕ»‘ΦΈΣ___ _
ΒΡ≥ΛΕ»‘ΦΈΣ___ _![]() .
.