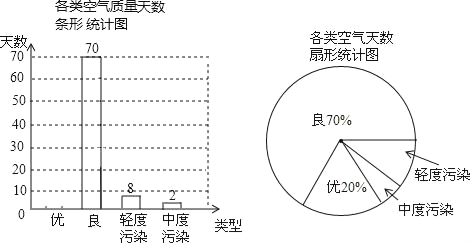
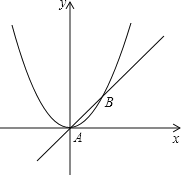
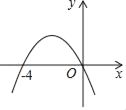
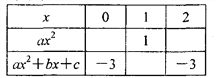
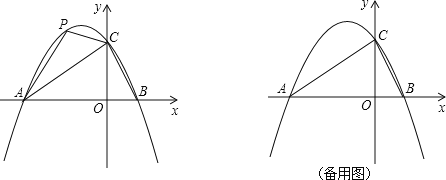��Ŀ����
����Ŀ���ھ���ABCD�У���P��AD�ϣ�AB=2��AP=1.ֱ�dzߵ�ֱ�Ƕ�����ڵ�P����ֱ�dzߵ����߷ֱ�AB��BC�ڵ�E��F������EF(��ͼ1).
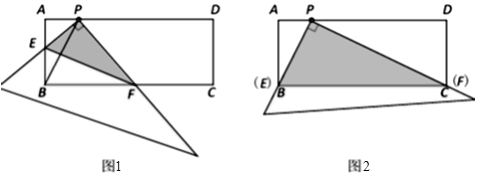
(1)����E���B�غ�ʱ����Fǡ�����C�غ�(��ͼ2).
����֤����APB�ס�DCP��
����PC��BC�ij�.
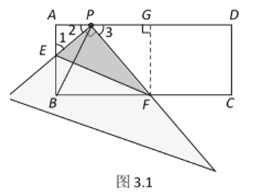
(2)̽������ֱ�dzߴ�ͼ2�е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E�͵�A�غ�ʱֹͣ.�����������(ͼ1�Ǹù��̵�ij��ʱ��)���۲졢���벢���
�� tan��PEF��ֵ�Ƿ����仯����˵������.
�� ��AE=x������PBF�ǵ���������ʱ����ֱ��д��x��ֵ.
���𰸡�(1)��֤������������PC=2![]() ��BC=5��(2)��tan��PEF��ֵ���䣻��x=
��BC=5��(2)��tan��PEF��ֵ���䣻��x=![]() ��x=
��x=![]() ��x=
��x=![]() .
.
��������
��1�����ɹ��ɶ�����BP�����û����ϵ֤����APB�ס�DCP�����������Ʊ���PC��DP, �ٸ���BC=AD=AP+DP�������BC�ij���
��2����tan��PEF��ֵ���䣮����Ϊ����F��FG��AD������Ϊ��G. ���ı���ABFG�Ǿ��Σ�ͬ��1���ķ���֤����APE�ס�GFP�������Ʊ�![]() ��������������Ǻ����Ķ�����ֵ�����������Ʊ���GP���پ����������BF����PBF�ǵ��������Σ�������������ۣ�(��) ��PB=PFʱ������BF=2AP��ֵ����BF=BPʱ��(��)����BP=
��������������Ǻ����Ķ�����ֵ�����������Ʊ���GP���پ����������BF����PBF�ǵ��������Σ�������������ۣ�(��) ��PB=PFʱ������BF=2AP��ֵ����BF=BPʱ��(��)����BP=![]() ��ֵ��(��) ��BF=PFʱ������PF=
��ֵ��(��) ��BF=PFʱ������PF=![]() �������xֵ.
�������xֵ.
�⣺(1)����ͼ3.2��
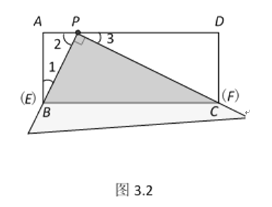
���ı���ABCD�Ǿ��Σ�
���A=��D=90����CD=AB=2��
����Rt��ABC��
��1+��2=90����BP=![]() .
.
�֡ߡ�BPC=90��,
���3+��2=90����
���1=��3.
���APB�ס�DCP.
������APB�ס�DCP.
��![]() ����
����![]() .
.
��PC=2![]() ��DP=4.
��DP=4.
��BC=AD=AP+DP=5.
(2)��tan��PEF��ֵ����.
�������£�
��ͼ3.1����F��FG��AD������Ϊ��G. ���ı���ABFG�Ǿ���.
���A=��PGF=90����FG=AB=2��
����Rt��APE����1+��2=90����
�֡ߡ�EPF=90��,���3+��2=90����
���1=��3.
���APE�ס�GFP��
��![]() .
.
����Rt��EPF��tan��PEF=![]() 2.
2.
��tan��PEF��ֵ����.
������APE�ס�GFP.
��![]() .
.
��GP=2AE=2x��
���ı���ABFG�Ǿ���.
��BF=AG=AP+GP=2x+1.
��PBF�ǵ��������Σ�������������ۣ�
(��)��PB=PFʱ����P��BF�Ĵ�ֱƽ������.
�� BF=2AP. ��2x+1=2��
��x=![]() .
.
(��)��BF=BPʱ��
BP=![]() BP=
BP=![]()
��2x+1=![]() .
.
��x=![]() .
.
(��)��BF=PFʱ��
��PF=![]() ��
��
��(2x)2+22=(2x+1)2��
��x=![]() .
.