题目内容
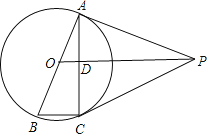
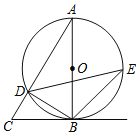
【题目】如图,已知△ABC中,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
(1)求证:BC为⊙O的切线;
(2)若E为![]() 中点,BD=12,sin∠BED=
中点,BD=12,sin∠BED=![]() ,求BE的长.
,求BE的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由圆周角定理和已知条件证出∠CBD+∠ABD=90°.得出∠ABC=90°,即可得出结论.
(2)连接AE.由圆周角定理得出∠BAD=∠BED,由三角函数定义求出直径AB=20.证出AE=BE.得出△AEB是等腰直角三角形.得出∠BAE=45°,由三角函数即可得出结果.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠A+∠ABD=90°.
又∵∠A=∠CBD,
∴∠CBD+∠ABD=90°.
∴∠ABC=90°.
∴AB⊥BC.
又∵AB是⊙O的直径,
∴BC为⊙O的切线.
(2)解:连接AE.如图所示:
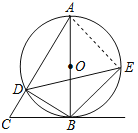
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°.
∵∠BAD=∠BED,
∴sin∠BAD=sin∠BED=![]() .
.
∴在Rt△ABD中,sin∠BAD=![]() ,
,
∵BD=12,
∴AB=20.
∵E为![]() 的中点,
的中点,
∴AE=BE.
∴△AEB是等腰直角三角形.
∴∠BAE=45°.
∴BE=AB×sin∠BAE=20×![]() =
=![]() .
.

练习册系列答案
相关题目