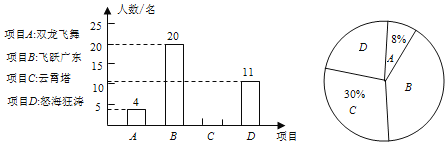
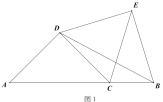
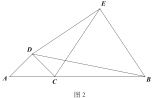
ЬтФПФкШн
ЁОЬтФПЁПФГЪадкЕГжабыЪЕЪЉЁАОЋзМЗіЦЖЁБеўВпЕФКХейЯТЃЌДѓСІПЊеЙПЦММЗіЦЖЙЄзїЃЌАяжњХЉУёзщНЈХЉИБВњЦЗЯњЪлЙЋЫОЃЌФГХЉИБВњЦЗЕФФъВњСПВЛГЌЙ§100ЭђМўЃЌИУВњЦЗЕФЩњВњЗбгУyЃЈЭђдЊЃЉгыФъВњСПxЃЈЭђМўЃЉжЎМфЕФКЏЪ§ЭМЯѓЪЧЖЅЕуЮЊдЕуЕФХзЮяЯпЕФвЛВПЗжЃЈШчЭМЂйЫљЪОЃЉЃЛИУВњЦЗЕФЯњЪлЕЅМлzЃЈдЊ/МўЃЉгыФъЯњЪлСПxЃЈЭђМўЃЉжЎМфЕФКЏЪ§ЭМЯѓЪЧШчЭМЂкЫљЪОЕФвЛЬѕЯпЖЮЃЌЩњВњГіЕФВњЦЗЖМФмдкЕБФъЯњЪлЭъЃЌДяЕНВњЯњЦНКтЃЌЫљЛёУЋРћШѓЮЊwЭђдЊЃЎЃЈУЋРћШѓ=ЯњЪлЖюЉЩњВњЗбгУЃЉ

ЃЈ1ЃЉЧыжБНгаДГіyгыxвдМАzгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓwгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛВЂЧѓФъВњСПЖрЩйЭђМўЪБЃЌЫљЛёУЋРћШѓзюДѓЃПзюДѓУЋРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉгЩгкЪмзЪН№ЕФгАЯьЃЌНёФъЭЖШыЩњВњЕФЗбгУВЛЛсГЌЙ§360ЭђдЊЃЌНёФъзюЖрПЩЛёЕУЖрЩйЭђдЊЕФУЋРћШѓЃП
ЁОД№АИЁПЃЈ1ЃЉy=![]() x2ЃЌz=Љ
x2ЃЌz=Љ![]() x+30ЃЛЃЈ2ЃЉW==Љ
x+30ЃЛЃЈ2ЃЉW==Љ![]() x2+30xЃЌФъВњСПЮЊ75ЭђМўЪБУЋРћШѓзюДѓЃЌзюДѓУЋРћШѓЮЊ1125ЭђдЊЃЛЃЈ3ЃЉНёФъзюЖрПЩЛёЕУ1080ЭђдЊЕФУЋРћШѓ.
x2+30xЃЌФъВњСПЮЊ75ЭђМўЪБУЋРћШѓзюДѓЃЌзюДѓУЋРћШѓЮЊ1125ЭђдЊЃЛЃЈ3ЃЉНёФъзюЖрПЩЛёЕУ1080ЭђдЊЕФУЋРћШѓ.
ЁОНтЮіЁП
ЃЈ1ЃЉНсКЯЭМЯѓЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіyгыxвдМАzгыxжЎМфЕФКЏЪ§ЙиЯЕЪНМДПЩЃЛЃЈ2ЃЉИљОнУЋРћШѓ=ЯњЪлЖюЉЩњВњЗбгУПЩЕУwгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛЃЈ3ЃЉСюy=0ЃЌНтЗНГЬЧѓЕУxЕФжЕЃЌИљОнЭМЯѓНсКЯyЕФШЁжЕЗЖЮЇЃЌЧѓЕУxЕФШЁжЕЗЖЮЇЃЌдйгЩЖўДЮКЏЪ§ЕФаджЪМДПЩНтД№.
ЃЈ1ЃЉЭМЂйПЩЕУКЏЪ§ОЙ§ЕуЃЈ100ЃЌ1000ЃЉЃЌ
ЩшХзЮяЯпЕФНтЮіЪНЮЊy=ax2ЃЈaЁй0ЃЉЃЌ
НЋЕуЃЈ100ЃЌ1000ЃЉДњШыЕУЃК1000=10000aЃЌ
НтЕУЃКa=![]() ЃЌ
ЃЌ
ЙЪyгыxжЎМфЕФЙиЯЕЪНЮЊy=![]() x2ЃЎ
x2ЃЎ
ЭМЂкПЩЕУЃККЏЪ§ОЙ§ЕуЃЈ0ЃЌ30ЃЉЁЂЃЈ100ЃЌ20ЃЉЃЌ
Щшz=kx+bЃЌдђ![]() ЃЌ
ЃЌ
НтЕУЃК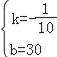 ЃЌ
ЃЌ
ЙЪzгыxжЎМфЕФЙиЯЕЪНЮЊz=Љ![]() x+30ЃЛ
x+30ЃЛ
ЃЈ2ЃЉW=zxЉy=Љ![]() x2+30xЉ
x2+30xЉ![]() x2
x2
=Љ![]() x2+30x
x2+30x
=Љ![]() ЃЈx2Љ150xЃЉ
ЃЈx2Љ150xЃЉ
=Љ![]() ЃЈxЉ75ЃЉ2+1125ЃЌ
ЃЈxЉ75ЃЉ2+1125ЃЌ
ЁпЉ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрЕБx=75ЪБЃЌWгазюДѓжЕ1125ЃЌ
ЁрФъВњСПЮЊ75ЭђМўЪБУЋРћШѓзюДѓЃЌзюДѓУЋРћШѓЮЊ1125ЭђдЊЃЛ
ЃЈ3ЃЉСюy=360ЃЌЕУ![]() x2=360ЃЌ
x2=360ЃЌ
НтЕУЃКx=ЁР60ЃЈИКжЕЩсШЅЃЉЃЌ
гЩЭМЯѓПЩжЊЃЌЕБ0ЃМyЁм360ЪБЃЌ0ЃМxЁм60ЃЌ
гЩW=Љ![]() ЃЈxЉ75ЃЉ2+1125ЕФаджЪПЩжЊЃЌ
ЃЈxЉ75ЃЉ2+1125ЕФаджЪПЩжЊЃЌ
ЕБ0ЃМxЁм60ЪБЃЌWЫцxЕФдіДѓЖјдіДѓЃЌ
ЙЪЕБx=60ЪБЃЌWгазюДѓжЕ1080ЃЌ
Д№ЃКНёФъзюЖрПЩЛёЕУУЋРћШѓ1080ЭђдЊЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ