题目内容
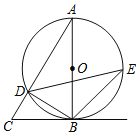
【题目】如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.

⑴ 求证:AE=AC;
⑵ 若AB⊥AC, F是BC的中点,试判断四边形AFCD的形状,并说明理由.
【答案】(1)见解析;(2)四边形AFCD是菱形,理由见解析
【解析】
(1)首先连接BD,根据等腰梯形的性质,可得AC=BD,易得四边形AEBD是平行四边形,由平行四边形的对边相等,即可得AE=BD,继而证得结论;
(2)由AB⊥AC,F是BC的中点,根据等腰梯形的性质,易求得∠ACB=30°,继而可证得AF=FC=CD=AD,则可判定四边形AFCD是菱形.
(1)连接BD
∵梯形ABCD是等腰梯形
∴AC=BD
∵BE=AD, AD∥BC
∴四边形AEBD是平行四边形
∴AE=BD,
∴AE=AC
(2)四边形AFCD是菱形, 理由是:
∵AB⊥AC, F是BC的中点
∴AF=CF,
∴∠FAC=∠FCA
∵AD=DC,
∴∠DAC=∠DCA
∵AD∥BC,
∴∠DAC=∠FCA
∴∠DCA=∠FAC
∴AF∥DC
∵AD∥BC,AF∥DC
∴四边形AFCD是平行四边形
又AD=DC
∴四边形AFCD是菱形

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目