题目内容
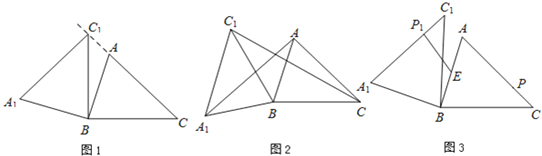
【题目】如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为16,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值之和.
【答案】(1)90° (2)25 (3)![]()
【解析】
(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,又由等腰三角形的性质,即可求得∠CC1A1的度数;
(2)由旋转的性质可得:△ABC≌△A1BC1,易证得△ABA1∽△CBC1,利用相似三角形的面积比等于相似比的平方,即可求得△CBC1的面积;
(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°;
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴![]() ,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1,
∴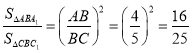 ,
,
∵S△ABA1=16,
∴S△CBC1=25;
(3)如图,过点B作BD⊥AC,D为垂足,
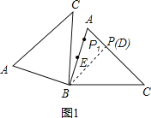
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=![]() ;
;
①当P在AC上运动至BP⊥AC时,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=![]() ﹣2;
﹣2;
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=2+5=7;
因此,线段EP1长度的最大值与最小值的和为:7+![]() ﹣2=
﹣2=![]() .
.

 开心蛙口算题卡系列答案
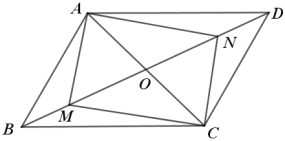
开心蛙口算题卡系列答案【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
【题目】我国淡水资源短缺问题十分突出,节约用水已成为各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区10户家庭的月用水量,结果如表所示:
月用水量(t) | 3 | 4 | 5 | 10 |
户数 | 4 | 2 | 3 | 1 |
这10户家庭月用水量的平均数、中位数及众数是( )
A. 4.5,3,4B. 3,4.5,4C. 4.5,4,3D. 4,4.5,3