Question

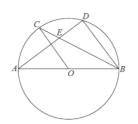
【题目】如图，AB为⊙O的直径，AC，BC是⊙O的两条弦，过点C作∠BCD＝∠A，CD交AB的延长线于点D．

（1）试说明：CD是⊙O的切线；

（2）若tanA＝，求的值；

（3）在（2）的条件下，若AB＝7，DE平分∠ADC交AC于点E，求ED的长．

Answer 1

【答案】（1）证明见解析；（2）；（3）

【解析】

（1）连接OC，由∠A＝∠BCD＝∠ACO且∠ACO＋∠OCB＝90°知∠BCD＋∠OCB＝90°，据此即可得证；

（2）先△ADC∽△CDB得＝＝，得出，从而得出，进而可得出答案；

（3）由（2）得AB＝7、BD＝9、CD＝12，证DE是∠ADC的平分线知＝＝，然后通过勾股定理求出AC,BC的长度，然后证得∠A＋∠EDA＝∠DEC＝45°，则△CDH为等腰直角三角形，由BCDH知∠CDH＝∠BCD，据此得tan∠CDH＝＝，继而得DH＝CD＝，DE＝DH．

解：（1）如图，连接OC，

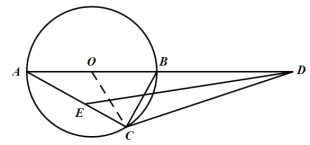
∵OA＝OC，

∴∠A＝∠ACO，

∵∠A＝∠BCD，

∴∠BCD＝∠ACO，

∵AB是⊙O的直径，

∴∠ACB＝90°，即∠ACO＋∠OCB＝90°，

∴∠BCD＋∠OCB＝90°，即∠OCD＝90°，

，

∴CD是⊙O的切线．

（2）∵∠BCD＝∠A，∠ADC＝∠ADC，

∴△ADC∽△CDB，

．

∵tanA＝＝，

∴，

，

，

∴．

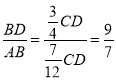（3）过点E作EM⊥AB于M，EN⊥DC交DC的延长线于N，过点D作DH⊥AC交AC延长线于点H，

，

．

，

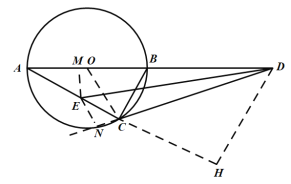
设 ，

，

，

解得 ，

∴．

∵DE是∠ADC的平分线，EM⊥AB，EN⊥DC，

∴EM＝EN，

∴＝=，

∴===，

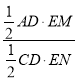∴EC．

∵∠BCD＝∠A，∠EDA＝∠EDC，且∠A＋∠BCD＋∠EDA＋∠EDC＝90°，

∴∠A＋∠EDA＝∠DEC＝45°，

∴△DEH为等腰直角三角形，

∴DE＝DH．

，

BCDH，

∴∠CDH＝∠BCD，

∴tan∠CDH＝＝，

∴DH＝CD＝12×＝，

则DE＝DH＝．