题目内容
如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD中心,O1O2⊥AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况共出现 次.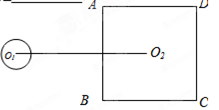

5
根据⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,设O1O2交圆O1于M,求出PM=4,得出圆O1与以P为圆心,以4为半径的圆相外切,即可得到答案.
解答:解:∵⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,

设O1O2交圆O1于M,
∴PM=8-3-1=4,
圆O1与以P为圆心,以4为半径的圆相外切,
∴有5次,依次是⊙O1在正方形ABCD外,与边AD相切,⊙O1在正方形ABCD内,与边AD相切,⊙O1在正方形ABCD内,与边CD相切,⊙O1在正方形ABCD内,与边CD相切,⊙O1在正方形ABCD外,与边BC相切;
故答案为:5.
解答:解:∵⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,

设O1O2交圆O1于M,
∴PM=8-3-1=4,
圆O1与以P为圆心,以4为半径的圆相外切,
∴有5次,依次是⊙O1在正方形ABCD外,与边AD相切,⊙O1在正方形ABCD内,与边AD相切,⊙O1在正方形ABCD内,与边CD相切,⊙O1在正方形ABCD内,与边CD相切,⊙O1在正方形ABCD外,与边BC相切;
故答案为:5.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在第一象限,⊙
在第一象限,⊙ 轴相切于点
轴相切于点 ,与
,与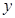 轴交于
轴交于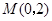 ,
, 两点,则点
两点,则点
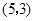
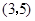

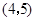

 的图像过点P,则
的图像过点P,则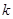 = .
= .
 是圆O的一条弦,
是圆O的一条弦, ,垂足为
,垂足为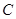 ,交圆O于点
,交圆O于点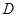 ,点
,点 在圆O上.(1)若
在圆O上.(1)若 ,求
,求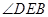 的度数;
的度数;
 ,
, ,求
,求 的两个根,则它们的圆心距
的两个根,则它们的圆心距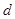 的取值范围是 .
的取值范围是 .
