题目内容
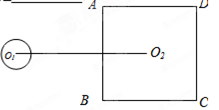
如图,直角梯形ABCD中,AD∥BC,∠B=90°,BC=2AB=2AD=4.以AB为直径作
⊙O,点P在梯形内的半圆弧上运动,则△CPD 的最小面积是_______________.

⊙O,点P在梯形内的半圆弧上运动,则△CPD 的最小面积是_______________.

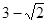
首先过点O作OE⊥CD交CD的延长线于E,OE交⊙O 于P,则△PCD就是所求的三角形,连接OC、OD,过点D作DF⊥BC于点F,由直角梯形ABCD中,AD∥BC,∠B=90°,BC=2AB=2AD=4.易求得△OCD的面积与CD的长,继而求得OE的长,则可求得PE的长,继而求得△CPD的最小面积.
解:过点O作OE⊥CD交CD的延长线于E,OE交⊙O 于P,则△PCD就是所求的三角形,连接OC、OD,过点D作DF⊥BC于点F,
∵直角梯形ABCD中,AD∥BC,∠B=90°,
∴∠A=∠B=∠BFD=90°,
∴四边形ABDF是矩形,
∴BF=AD,DF=AB,
∵BC=2AB=2AD=4,
∴AD=AB=2,
∵以AB为直径作⊙O,
∴OA=OB=1,
∴S梯形ABCD= (AD+BC)?AB=
(AD+BC)?AB= ×(2+4)×2=6,S△OAD=
×(2+4)×2=6,S△OAD= OA?AD=
OA?AD= ×1×2=1,S△OBC=
×1×2=1,S△OBC= OB?BD=
OB?BD= ×1×4=2,
×1×4=2,
∴S△ODC=S梯形ABCD-S△OAD-S△OBC=6-1-2=3,
在Rt△DFC中,CF=BC-BF=4-2=2,DF=AB=2,
∴CD=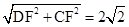 ,
,
∵S△OCD= CD?OE=3,
CD?OE=3,
∴OE= ,
,
∴PE=OE-OP= -1,
-1,
∴S△CPD= CD?PE=
CD?PE= ×2
×2 ×(
×( -1)=3-
-1)=3- .
.
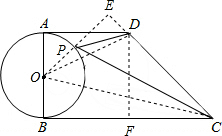
故答案为:3-
解:过点O作OE⊥CD交CD的延长线于E,OE交⊙O 于P,则△PCD就是所求的三角形,连接OC、OD,过点D作DF⊥BC于点F,

∵直角梯形ABCD中,AD∥BC,∠B=90°,
∴∠A=∠B=∠BFD=90°,
∴四边形ABDF是矩形,
∴BF=AD,DF=AB,
∵BC=2AB=2AD=4,
∴AD=AB=2,
∵以AB为直径作⊙O,
∴OA=OB=1,
∴S梯形ABCD=
 (AD+BC)?AB=
(AD+BC)?AB= ×(2+4)×2=6,S△OAD=
×(2+4)×2=6,S△OAD= OA?AD=
OA?AD= ×1×2=1,S△OBC=
×1×2=1,S△OBC= OB?BD=
OB?BD= ×1×4=2,
×1×4=2,∴S△ODC=S梯形ABCD-S△OAD-S△OBC=6-1-2=3,
在Rt△DFC中,CF=BC-BF=4-2=2,DF=AB=2,
∴CD=
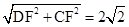 ,
,∵S△OCD=
 CD?OE=3,
CD?OE=3,∴OE=
 ,
,∴PE=OE-OP=
 -1,
-1,∴S△CPD=
 CD?PE=
CD?PE= ×2
×2 ×(
×( -1)=3-
-1)=3- .
.故答案为:3-


练习册系列答案
相关题目
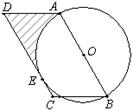
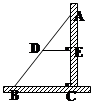
 .
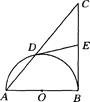
.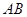 为⊙O的直径,点
为⊙O的直径,点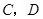 在⊙O上,
在⊙O上,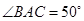 ,则
,则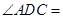 ____度
____度