题目内容
如图,在平面直角坐标系中,点 在第一象限,⊙
在第一象限,⊙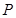 与
与 轴相切于点
轴相切于点 ,与
,与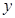 轴交于
轴交于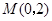 ,
, 两点,则点
两点,则点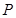 的坐标是( ).
的坐标是( ).

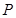 在第一象限,⊙
在第一象限,⊙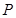 与
与 轴相切于点
轴相切于点 ,与
,与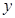 轴交于
轴交于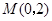 ,
, 两点,则点
两点,则点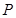 的坐标是( ).
的坐标是( ).
A.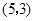 | B.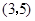 | C. | D.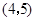 |
D
分析:根据已知条件,纵坐标易求;再根据切割线定理即OQ2=OM?ON求OQ可得横坐标.
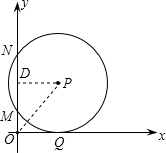
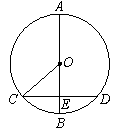
解:过点P作PD⊥MN于D,连接PO.
∵⊙P与x轴相切于点Q,与y轴交于M(0,2),N(0,8)两点,
∴OM=2,NO=8,
∴NM=6,
∵PD⊥NM,
∴DM=3
∴OD=5,
∴OQ2=OM?ON=2×8=16,OQ=4.
∴PD=4,PQ=OD=3+2=5.
即点P的坐标是(4,5).
故选D.
点评:本题综合考查了图形的性质和坐标的确定,是综合性较强,难度中等的综合题,关键是根据垂径定理确定点P的纵坐标,利用切割线定理确定横坐标.

解:过点P作PD⊥MN于D,连接PO.
∵⊙P与x轴相切于点Q,与y轴交于M(0,2),N(0,8)两点,
∴OM=2,NO=8,
∴NM=6,
∵PD⊥NM,
∴DM=3
∴OD=5,
∴OQ2=OM?ON=2×8=16,OQ=4.
∴PD=4,PQ=OD=3+2=5.
即点P的坐标是(4,5).
故选D.
点评:本题综合考查了图形的性质和坐标的确定,是综合性较强,难度中等的综合题,关键是根据垂径定理确定点P的纵坐标,利用切割线定理确定横坐标.

练习册系列答案
相关题目
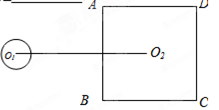
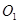 和⊙
和⊙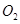 的半径分别是一元二次方程
的半径分别是一元二次方程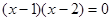 的两根且
的两根且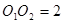 ,则⊙
,则⊙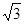 cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )
cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )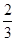 cm
cm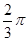 cm
cm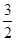 cm
cm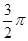 cm
cm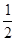 ,求⊙O的直径.
,求⊙O的直径.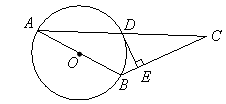


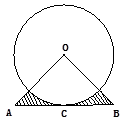
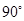 ,OA=OB=
,OA=OB=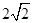 ,以点O为圆心的圆与AB相切于点C,则图中阴影部分的面积是______________.
,以点O为圆心的圆与AB相切于点C,则图中阴影部分的面积是______________.