题目内容
如图：已知在
中，AD平分∠BAC，
为
边的中点，过点作
，垂足分别为
。
（1）求证：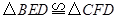
；
（2）若
，求证：四边形
是正方形。
中，AD平分∠BAC，为边的中点，过点作，垂足分别为。（1）求证：
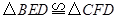；（2）若
，求证：四边形是正方形。见解析
试题分析：（1）由AD平分∠BAC，
，根据角平分线的性质即可得到DE=DF，再由为边的中点，即可证得结论；（2）由
，，可得四边形是矩形，再结合DE=DF即可证得结论。（1）∵AD平分∠BAC，
，∴DE=DF（角平分线上的点到角两边的距离相等），
∵
为边的中点，∴BD=CD，
∴
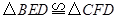；（2）∵
，，∴四边形
是矩形，∵DE=DF，
∴矩形
是正方形.点评：判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等；②先说明它是菱形，再说明它有一个角为直角．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
的对角线
的垂直平分线与边
，
分别交于点
，
，四边形
是否是菱形。（6分）
