Question

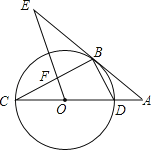
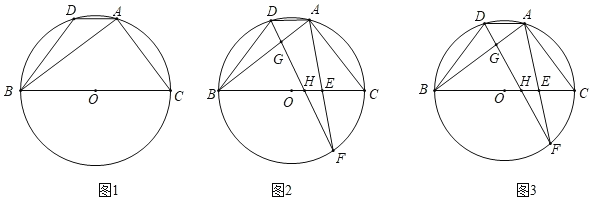
【题目】已知：△ABC内接于⊙O，点D为弧AB上一点，连接AD，BD，且AC=BD．

（1）如图1，求证：AD∥BC；

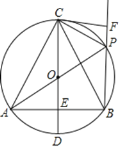
（2）如图2，点E为BC上一点，连接AE并延长交⊙O于点F，连接DF分别交AB，BC于点G，H，∠BAD+∠CAF=∠BGH，求证：AD=AG；

（3）如图3，在（2）的条件下，当∠BAF=60°，AE=EF，BH=6时，求BE的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）7．

【解析】

（1）由AC=BD推出，进一步推出∠ABC=∠DAB，由平行线的判定即可写出结论； （2）如图2，连接BF，先证∠FBG=∠BGF，再证∠FDA=∠AGD，即可得出结论； （3）如图3，延长BD、FA交于点M，过点B作BN⊥AF于点N，先证AD=AG，AD=AM，BE=EM，再证△FEH∽△FAD，推出AD=2HE，设HE=，则AD=，AG=AM=，BE=BH+HE=，所以BA=BG+GA=，EA=EM-AM=，在Rt△ABN中，求出AN=AB=，BN=AN=，所以NE=EM-AM-AN=，最后在Rt△BNE中，由可求出的值，即可写出BE的长．

（1）证明：∵AC=BD，∴，

∴∠ABC=∠DAB，∴AD∥BC；

（2）如图2，连接BF，因为，则∠CAF=∠CBF．

， ∠BAD=∠ABC，

∴∠BAD+∠CAF=∠CBF+∠ABC=∠FBG．

∵∠BAD+∠CAF=∠BGF，∴∠FBG=∠BGF．

∵∠FBG=∠FDA，∠BGF=∠AGD，

∴∠FDA=∠AGD，∴AD=AG；

（3）如图3，延长BD、FA交于点M，过点B作BN⊥AF于点N．

∵，∴∠BDF=∠BAF=60°，

设∠DAG=2α．

∵AD=AG，∴∠ADG=90°﹣α，∠DAM=120°﹣2α，∴∠ADM=30°+α，∴∠DMA=∠ADM=30°+α，∴AD=AM．

∵AD∥BC，∴∠ADM=∠EBD，∴∠EBD=∠DMA，∴BE=EM．

∵，∠BGH=∠BHG，∴BG=BH=6．

∵AD∥BC，∴△FEH∽△FAD，∴．

∵AE=EF，∴，∴，∴AD=2HE，

设HE=x，则AD=2x，AG=AM=2x，BE=BH+HE=6+x，

∴BA=BG+GA=6+2x，EA=EM﹣AM=6﹣x，

在Rt△ABN中，∠BAN=60°，∠ABN=30°，

∴，，

∴NE=EM﹣AM﹣AN=3﹣2x，

在Rt△BNE中，BN2+NE2=BE2，

即，

解得：（取正值），∴．