题目内容
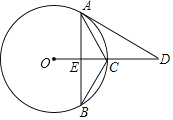
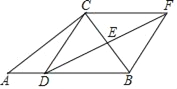
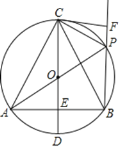
【题目】如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为![]() 上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,
上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,![]() 的值始终等于
的值始终等于![]() .则下列说法正确的是( )
.则下列说法正确的是( )
A.①,②都对B.①对,②错C.①错,②对D.①,②都错
【答案】A
【解析】
作CM⊥AP于M,连接AD,根据线段垂直平分线的性质得到AO=AD,证明△AOD是等边三角形,求出∠D=∠ABC=60°,根据垂径定理得到CA=CB,从而证得①;利用圆周角定理求出∠CPF=60°,根据角平分线的性质得到CF=CM,证明Rt△CPF≌Rt△CPM得到PF=PM,证明Rt△AMC≌Rt△BFC得到AM=BF,求出![]() 再根据三角函数求出
再根据三角函数求出![]() 得到②正确.
得到②正确.
如图,作CM⊥AP于M,连接AD.
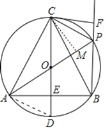
∵AE⊥OD,OE=DE,
∴AO=AD,
∵OA=OD,
∴AO=AD=OD,
∴△AOD是等边三角形,
∴∠D=∠ABC=60°,
∵CD⊥AB,
∴AE=EB,
∴CA=CB,
∴△ABC是等边三角形,故①正确,
∵∠CPA=∠ABC=60°,∠APB=∠ACB=60°,
∴∠CPF=180°﹣60°﹣60°=60°,
∵∠CPM=∠CPF=60°,CF⊥PF,CM⊥PA,
∴CF=CM,
∵PC=PC,∠CFP=∠CMP,
∴Rt△CPF≌Rt△CPM(HL),
∴PF=PM,
∵AC=BC,CM=CF,∠AMC=∠CFB=90°,
∴Rt△AMC≌Rt△BFC(HL),
∴AM=BF,
∴AP﹣PB=PM+AM﹣(BF﹣PF)=2PM=2PF,
∴![]() ,
,
在Rt△CPF中,
∵∠CPF=60°,∠CFP=90°,
![]() ,
,
![]() ,
,
∴![]() ,故②正确,
,故②正确,
故选:A.

练习册系列答案
相关题目