��Ŀ����
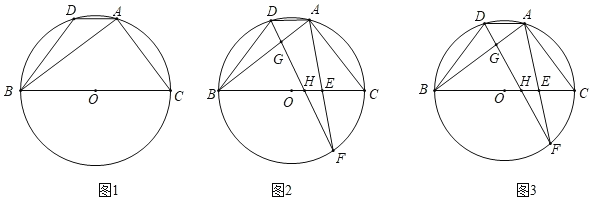
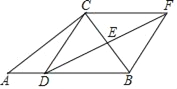
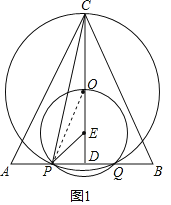
����Ŀ����ABC�У�CA��CB��AB��![]() ��CD��AB�ڵ�D��CD��5����O�͵�E���߶�CD�ϣ�ED��1����P�ڱ�AB�ϣ���EΪԲ�ģ�EPΪ�뾶��Բ��AB�ߵ���һ������Ϊ��Q����P�ڵ�Q����ࣩ����OΪԲ�ģ�OCΪ�뾶��ԲOǡ�þ���P��Q���㣬����CP�����߶�AP�ij���Ϊx��
��CD��AB�ڵ�D��CD��5����O�͵�E���߶�CD�ϣ�ED��1����P�ڱ�AB�ϣ���EΪԲ�ģ�EPΪ�뾶��Բ��AB�ߵ���һ������Ϊ��Q����P�ڵ�Q����ࣩ����OΪԲ�ģ�OCΪ�뾶��ԲOǡ�þ���P��Q���㣬����CP�����߶�AP�ij���Ϊx��
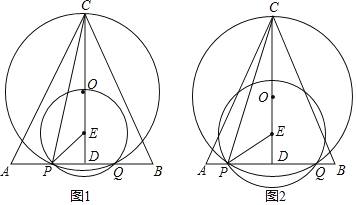
��1����ԲEǡ�þ�����Oʱ����ԲE�İ뾶��
��2������CQ�����PCQ������ֵΪy����y��x�ĺ�����ϵʽ��������
��3������PED��3��PCE����S��PCQ��ֵ��
���𰸡���1��![]() ��5����2��y��
��5����2��y��![]() ��
��![]() ��x��
��x��![]() ������3��
������3��![]()
��������
��1������OP������E�İ뾶Ϊr������OP2��OD2��PE2��DE2�г����̼���������ۣ�
��2������OQ�����ݵȱ߶ԵȽǿɵá�OCQ����OQC��Ȼ��֤����PCQ����DOQ�����ݹ��ɶ��������Ƴ�m��x�Ĺ�ϵ��������������Ǻ����������y��x�ĺ�����ϵʽ��
��3������CQ��OP������O��OH��CP��H����CG��PE��G�����������������ж��ֱ�֤����EPO�ס�ECP����CHO�ס�CDP����OC��OP��m���������������ε������г�����ʽ�������m��ֵ���Ӷ����PQ��CD������������ۣ�
�⣺��1����ͼ1������OP������E�İ뾶Ϊr����PE��OE��r��OP��OC��4��r��OD��r+1��
��CD��AB��
��OP2��OD2��PE2��DE2��
����4��r��2����r+1��2��r2��12��
���![]() ����ȥ����
����ȥ����![]() ��
��
��ԲE�İ뾶r��![]() ��5��
��5��
��2����ͼ2������OQ��
��OQ��OC��
���OCQ����OQC
�ߡ�DOQ����OCQ+��OQC
���DOQ��2��OCQ
�ߡ�PCD����QCD
���PCQ��2��QCD
���PCQ����DOQ
��OC��OQ��m����OD��5��m��
�ɹ��ɶ�����DQ2��m2����5��m��2��10m��25��
����֪��AP��x��
��DQ��![]() ��x��
��x��
��OD��5��m��![]() ��
��![]() ��
��
��y��tan��PCQ��tan��DOQ��![]() ��
��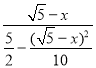 ��
��![]()
��![]()
��![]() ��x��
��x��![]() ��
��
��y��x�ĺ�����ϵʽΪ y��![]() ��
��![]() ��x��
��x��![]() ����
����
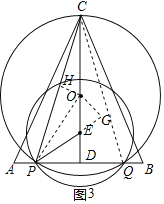
��3����ͼ3������CQ��OP������O��OH��CP��H����CG��PE��G��
��OC��OP��
���PCE����OPC��CH��![]() CP
CP
�ߡ�PED��3��PCE��
���OPE����OPC����PCE��
���EPO�ס�ECP��OH��OG��
��OC��OP��m��
�ߡ�CHO����CDP��90�㣬
���CHO�ס�CDP
��![]() ����
����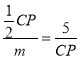
��CP2��10m��CP��![]() ��PD2��10m��25��PE2��10m��24��
��PD2��10m��25��PE2��10m��24��
��![]() ��
��
��![]()
��![]() ��
��
��ã�m1��0����ȥ����![]() ��
��
��PD��![]() ��
��![]() ��PQ��2PD��
��PQ��2PD��![]()
��![]() ��
��![]() ��
��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�����Ŀ��ij��˾����һ�ֽ���Ϊ20Ԫ/���ļ���������������y������������ۼ۸�x��Ԫ/�����ı仯���±���
�۸�x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
������y������� | �� | 5 | 4 | 3 | 2 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ��
��1���۲첢�������е�y��x֮��Ķ�Ӧ��ϵ������ѧ����һ�κ�������������������κ������й�֪ʶд��y���������x��Ԫ/�����ĺ�������ʽ��
��2������ù�˾�������ּ������ľ�������z����Ԫ�������ۼ۸�x��Ԫ/�����ĺ�������ʽ�����ۼ۸�Ϊ����Ԫʱ��������������ֵ�Ƕ��٣�
��3���ù�˾Ҫ�������ܵ���40��Ԫ����д�����ۼ۸�x��Ԫ/������ȡֵ��Χ�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ����Ԫ��