Question

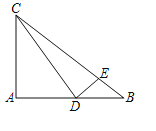
【题目】在Rt△ABC中，∠C=90°，AC=2，BC=4，点D、E分别是边BC、AB的中点，将△BDE绕着点B旋转，点D、E旋转后的对应点分别为点D′、E′，当直线D′E′经过点A时，线段CD′的长为_____．

Answer 1

【答案】或

【解析】

分两种情况：①点A在ED的延长线上时；②点A在线段DE的延长线上时；然后分类讨论，求出线段BD的长各是多少即可．

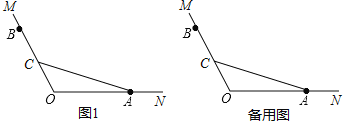
解：如图1，当点A在ED的延长线上时，

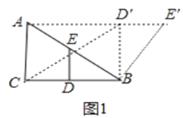
∵∠C=90°，AC=2，BC=4，

∴AB=，

∵点D、E分别是边BC、AB的中点，

∴DE∥AC，DE=AC=1， BD=BC=2，

∴∠EDB=∠ACB=90°

∵将△BDE绕着点B旋转，

∴∠BD′E′=∠BDE=90°，D′E′=DE=1，BD=BD=2，

∵在Rt△ABC和Rt△BAD′中，

D′B=AC=2，AB=BA，

即,

∵Rt△ABC≌Rt△BAD′（HL），

∴AD′=BC，且AC=D′B，

∴四边形ACBD′是平行四边形，且∠ACB=90°，

∴四边形ACBD′是矩形，

∴CD=AB=2；

如图2，当点A在线段D′E′的延长线上时，

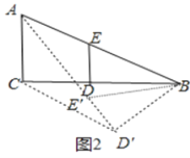
∵∠AD′B=90°，

∴AD′=，

∴AE=AD′-DE′=3，

∵将△BDE绕着点B旋转，

∴∠ABC=∠EBD，

∵，

∴△ABE∽△BCD′

∴，

∴，

，

故答案为：或．