Question

【题目】方程 7x (k 13)x k 2 0 ( k 是实数)有两个实数跟 a，b ，且 0 a 1 b 2 ，那么 k 的取值范围是_____．

Answer 1

【答案】-4＜k＜-2

【解析】

设y= 7x (k 13)x k 2 ( k 是实数)，由7＞0和已知条件画出二次函数的图象，可得当x=0时，y＞0；当x=1时，y＜0，当x=2时，y＞0，然后列出关于k的不等式组即可求出结论．

解：设y= 7x (k 13)x k 2 ( k 是实数)，由7＞0，原方程有两个实数跟 a，b ，且 0 a 1 b 2 ，

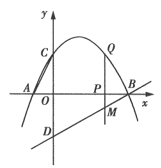
∴二次函数y= 7x (k 13)x k 2 的图象与x轴的交点为（a，0）和（b，0）且 0 a 1 b 2 ，画出其大致图象，如下所示

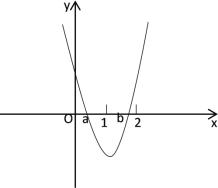
根据图象可得：当x=0时，y＞0；当x=1时，y＜0，当x=2时，y＞0

即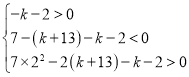

解得：-4＜k＜-2

故答案为：-4＜k＜-2．