题目内容
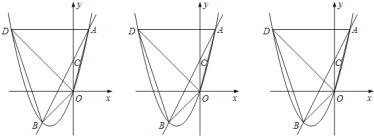
【题目】在如图的直角坐标系中,已知点A(1,0)、B(0,﹣2),将线段AB绕点A按逆时针方向旋转90°至AC,若抛物线y=﹣![]() x2+bx+2经过点C.
x2+bx+2经过点C.
(1)求抛物线的解析式;
(2)如图,将抛物线平移,当顶点至原点时,过Q(0,﹣2)作不平行于x轴的直线交抛物线于E、F两点,问在y轴的正半轴上是否存在一点P,使△PEF的内心在y轴上?若存在,求出点P的坐标;若不存在,说明理由.
(3)在抛物线上是否存在一点M,使得以M为圆心,以![]() 为半径的圆与直线BC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
为半径的圆与直线BC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
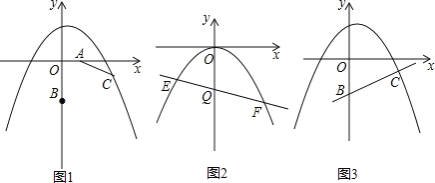
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)存在,P(0,2);(3)存在,点M的坐标为(﹣2,﹣1)或(
x+2;(2)存在,P(0,2);(3)存在,点M的坐标为(﹣2,﹣1)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() )
)
【解析】
(1)根据题意得出△AOB≌△CDA,从而求得OA=CD=1,AD=OB=2,即可求得C的坐标,然后把C的坐标代入抛物线的解析式即可求得b;
(2)将抛物线平移,当顶点至原点时,解析式为y=﹣![]() x2,设EF的解析式为y=kx﹣2(k≠0).假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.由△PEF的内心在y轴上,得出∠GEP=∠EPQ=∠QPF=∠HFP,那么△GEP∽△HFP,根据相似三角形对应边成比例以及根与系数的关系即可求解;
x2,设EF的解析式为y=kx﹣2(k≠0).假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.由△PEF的内心在y轴上,得出∠GEP=∠EPQ=∠QPF=∠HFP,那么△GEP∽△HFP,根据相似三角形对应边成比例以及根与系数的关系即可求解;
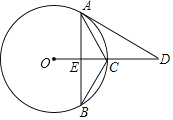
(3)根据B、C坐标根据待定系数法求得解析式,求得直线与x轴的解得坐标,在y轴上去一点K,作KS⊥BC于S,使KS=![]() ,易证得△BOG∽△BSK,由对应边成比例求得BK的出,既然求得K的坐标,过K点作BC平行线交抛物线的交点即为M点,求得平行线的解析式,然后和抛物线的解析式联立方程即可求得.
,易证得△BOG∽△BSK,由对应边成比例求得BK的出,既然求得K的坐标,过K点作BC平行线交抛物线的交点即为M点,求得平行线的解析式,然后和抛物线的解析式联立方程即可求得.
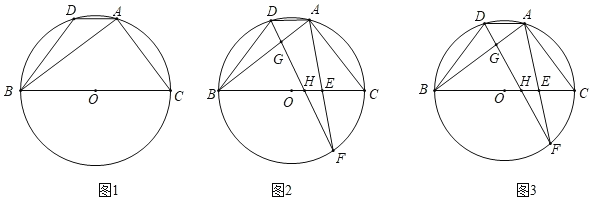
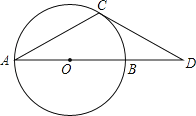
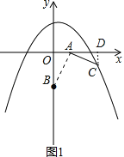
解:(1)如图1,∵点A(1,0)、B(0,﹣2),将线段AB绕点A按逆时针方向旋转90°至AC,
∴AB=AC,∠BAC=90°
连接AB,作CD⊥OD于D,
∴∠AOB=∠CDA=∠BAC=90°,
∴∠OBA+∠OAB=90°,∠DAC+∠OAB=90°
∴∠OBA=∠DAC
∴△AOB≌△CDA,
∴OA=CD,AD=OB,
∴C(3,﹣1),
∵抛物线y=﹣![]() x2+bx+2经过点C.
x2+bx+2经过点C.
∴﹣1=﹣![]() ×9+3b+2,
×9+3b+2,
解得b=![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)将抛物线平移,当顶点至原点时,抛物线为y=﹣![]() x2,设EF的解析式为y=kx﹣2(k≠0).
x2,设EF的解析式为y=kx﹣2(k≠0).
假设存在满足题设条件的点P(0,t),
如图2,过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.
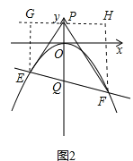
∵△PEF的内心在y轴上,
∴∠GEP=∠EPQ=∠QPF=∠HFP,
∴△GEP∽△HFP,
∴GP:PH=GE:HF,
∴﹣xE:xF=(t﹣yE):(t﹣yF)=(t﹣kxE+2):(t﹣kxF+2),
∴2kxExF=(t+2)(xE+xF),
联立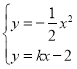
得x2+2kx﹣4=0,xE、xF是该一元二次方程的解
∴xE+xF=﹣2k,xExF=﹣4,
∴2k(﹣4)=(t+2)(﹣2k),
∵k≠0,
∴t=2,
∴y轴的正半轴上存在点P(0,2),使△PEF的内心在y轴上;
(3)∵B(0,﹣2),C(3,﹣1),
设直线BC的解析式为y=mx﹣2,
∴﹣1=3m﹣2,
∴m=![]() ,
,
∴y=![]() x﹣2,
x﹣2,
∴直线BC与x轴的交点G(6,0),

∴OB=2,OG=6,
∴BG=![]() =2
=2![]() ,在y轴上取一点K,作KS⊥BC于S,使KS=
,在y轴上取一点K,作KS⊥BC于S,使KS=![]() ,
,
∵∠BOG=∠BSK=90°,∠OBG=∠SBK,
∴△BOG∽△BSK,
∴![]() ,即
,即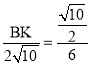 ,
,
∴BK=![]() ,
,
∴OK=![]() 或
或![]() ,
,
∴K(0,﹣![]() )或(0,﹣
)或(0,﹣![]() )
)
作KM∥BC交抛物线与M,
∴直线KM为y=![]() x﹣
x﹣![]() 或y=
或y=![]() x﹣
x﹣![]() ,
,
解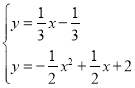
得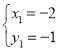 ,
,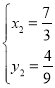 ,
,
解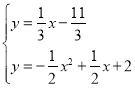
得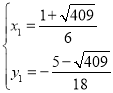 或
或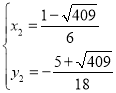 ,
,
∴在抛物线上存在一点M,使得以M为圆心,以![]() 为半径的圆与直线BC相切,点M的坐标为(﹣2,﹣1)或(
为半径的圆与直线BC相切,点M的坐标为(﹣2,﹣1)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).

 轻松暑假总复习系列答案
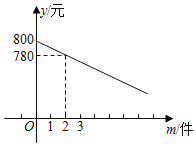
轻松暑假总复习系列答案【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.