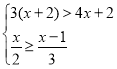题目内容
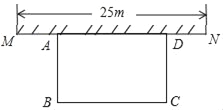
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料.
(1)设计一种砌法,使矩形花园的面积为300m2.
(2)当BC为何值时,矩形ABCD的面积有最大值?并求出最大值.
【答案】(1)见解析;(2) BC长为25米时,最大值为![]() .
.
【解析】
(1)根据题意可以得到相应的一元二次方程,从而可解答本题;(2)根据题意可以得到面积与矩形一边长的关系式,然后化为顶点式,注意求出的边长要符合题意.
:(1)设AB为xm,则BC为(50-2x)m,
x(50-2x)=300,
解得,x1=10,x2=15,
当x1=10时50-2x=30>25(不合题意,舍去),
当x2=15时50-2x=20<25(符合题意),
答:当砌墙宽为15米,长为20米时,花园面积为300平方米;
(2)设AB为xm,矩形花园的面积为ym2,
则y=x(50-2x)=-2(x-![]() )2+
)2+![]() ,
,
∴x=![]() 时,此时y取得最大值,50-2x=25符合题意,此时y=
时,此时y取得最大值,50-2x=25符合题意,此时y=![]() ,
,
即当砌墙BC长为25米时,矩形花园的面积最大,最大值为![]() .
.

练习册系列答案
相关题目