题目内容
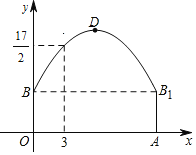
【题目】如图,直线![]() 与双曲线
与双曲线![]() 在第一象限内交于
在第一象限内交于![]() 、
、![]() 两点,已知
两点,已知![]() ,
,![]() .
.

(1)![]() __________,
__________,![]() ____________________,
____________________,![]() ____________________.
____________________.
(2)直接写出不等式![]() 的解集;
的解集;
(3)设点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 是
是![]() 轴上一点,求
轴上一点,求![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() .(2)
.(2)![]() 或
或![]() .(3)当
.(3)当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]()
【解析】
(1)先求出反比例函数解析式,进而求出点A坐标,最后用待定系数法,即可得出结论;
(2)直接利用函数图象得出结论;
(3)先设出点P坐标,进而表示出△PED的面积,即可得出结论.
解:(1)∵点B(2,1)在双曲线![]() 上,
上,
∴k2=2×1=2,
∴双曲线的解析式为y2=![]() ,
,
∵A(1,m)在双曲线y2=![]() 上,
上,
∴m=1×2=2,
∴A(1,2),
∵直线AB:y1=k1x+b过A(1,2)、B(2,1)两点,
∴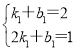 ,
,
∴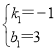 ,
,
∴直线AB的解析式为:y=x+3;
故![]() ,
,![]() ,
,![]()
故答案为:-1;2;3;
(2)根据函数图象得,不等式y2>y1的解集为0<x<1或x>2;
(3)设点![]() ,且
,且![]() ,
,
则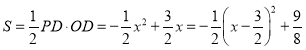
![]()
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]()

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目