题目内容
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
【答案】145
【解析】
先画出示意图,由相似三角形的判定可知,在△ABD和△DBC中,已知∠ABD=∠CBD,所以需另一组对应角相等,若∠A=∠C,则△ABD与△DBC全等不符合题意,所以必定有∠A=∠BDC,再根据四边形的内角和为360°列式求解.
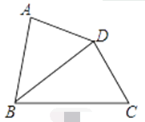
解:根据题意画出示意图,已知∠ABD=∠CBD,
△ABD与△DBC相似,但不全等,
∴∠A=∠BDC,∠ADB=∠C.
又∠A+∠ABC+∠C+∠ADC=360°,
∴2∠ADB+2∠BDC+∠ABC=360°,
∴∠ADB+∠BDC=145°,
即∠ADC=145°.

练习册系列答案
相关题目