��Ŀ����
����Ŀ����ѧϰ�����Ĺ����У����Ǿ�������ȷ�������ı���ʽ�������ú���ͼ���о������ʩ������ú��������������ѧϰ���̣���������������ѧϰ���̣������������������⣺�ں���y��ax3��bx+2�У���x����1ʱ��y��4����x����2ʱ y��0��
��1��������֪������֪��������ı���ʽ�� ����
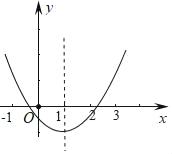
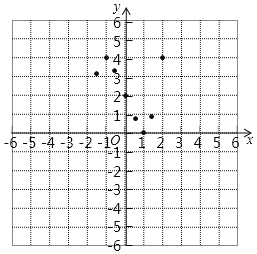
��2������������IJ��ֵ㣬�����ú���ͼ��
��3���۲�����ͼ�ش��������⣺
�ٸ�ͼ����ڵ��� �������ĶԳƣ�
�ڵ�xȡ��ֵʱ��y����x���������С��
����ֱ��y��c���ͼ����3�����㣬ֱ��д��c��ȡֵ��Χ��
���𰸡���1��y��x3��3x+2����2������������3����(0��-2)���ک�1��x��1����0��c��4
��������
��1�����ô���ϵ����������⼴�ɣ�
��2��������㷨��������ͼ�ɣ�
��3���������ν�ϵ�˼�������⼴�ɣ�
�⣺��1�������⣺![]() ����ã�
����ã�![]() ��
��
�ຯ������ʽΪ��y��x3��3x+2��
�ʴ�Ϊ��y��x3��3x+2��
��2������ͼ����ͼ��ʾ��

��3���ٹ۲�ͼ���֪������ͼ����ڣ�0��2�������ĶԳƣ�
�ʴ�Ϊ����0����2����
�ڹ۲�ͼ���֪������1��x��1ʱ��y����x���������С��
�۹۲�ͼ���֪����ֱ��y��c���ͼ����3�����㣬c��ȡֵ��ΧΪ0��c��4��

 һ����������ϵ�д�
һ����������ϵ�д�