题目内容
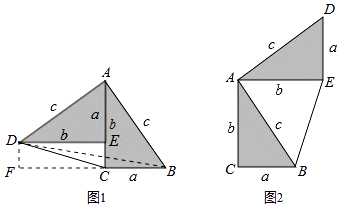
【题目】图1是一张可以折叠的小床展开后支撑起来放在地面的示意图，此时点A、B、C在同一直线上，且∠ACD=90°，图2是小床支撑脚CD折叠的示意图，在折叠过程中，△ACD变形为四边形ABC′D′，最后折叠形成一条线段BD″． 
（1）小床这样设计应用的数学原理是 ．
（2）若AB：BC=1：4，则tan∠CAD的值是 ．
【答案】
（1）三角形具有稳定性
（2）
【解析】解：（1.）小床这样设计应用的数学原理是：三角形具有稳定性； 所以答案是：三角形具有稳定性；
（2.）∵AB：BC=1：4，
∴设AB=x，DC=y，则BC=4x，C″D″=y，
由图形可得：BC″=4x，则AC″=3x，AD=AD″=3x+y，
故AC2+DC2=AD2 ， 即（5x）2+y2=（3x+y）2 ，
解得：y= 
x，
则tan∠CAD的值是： 
= 
= ．
所以答案是： ．
【考点精析】本题主要考查了翻折变换（折叠问题）的相关知识点，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．
练习册系列答案
相关题目
