题目内容
【题目】如图，在矩形ABCD中，E为CD的中点，F为BE上的一点，连结CF并延长交AB于点M，MN⊥CM交射线AD于点N．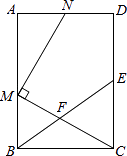 
（1）当F为BE中点时，求证：AM=CE；
（2）若 
=2，求 
的值；
（3）若 =n，当n为何值时，MN∥BE？
【答案】
（1）解：当F为BE中点时，如图1，则有BF=EF．
∵四边形ABCD是矩形，
∴AB=DC，AB∥DC，
∴∠MBF=∠CEF，∠BMF=∠ECF．
在△BMF和△ECF中，
，
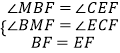∴△BMF≌△ECF，
∴BM=EC．
∵E为CD的中点，
∴EC= 
DC，
∴BM=EC= DC= AB，
∴AM=BM=EC
（2）解：如图2所示：
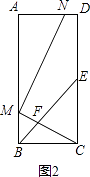
设MB=a，
∵四边形ABCD是矩形，
∴AD=BC，AB=DC，∠A=∠ABC=∠BCD=90°，AB∥DC，
∴△ECF∽△BMF，
∴ 
=2，
∴EC=2a，
∴AB=CD=2CE=4a，AM=AB﹣MB=3a．
∵ 
=2，
∴BC=AD=2a．
∵MN⊥MC，
∴∠CMN=90°，
∴∠AMN+∠BMC=90°．
∵∠A=90°，
∴∠ANM+∠AMN=90°，
∴∠BMC=∠ANM，
∴△AMN∽△BCM，
∴ 
，
∴ 
= 
，
∴AN= 
a，ND=AD﹣AN=2a﹣ a= a，
∴ 
= 
=3
（3）解：当 
=n时，如图3：
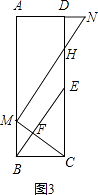
设MB=a．
∵△MFB∽△CFE，
∴ 
= 
，即 
，解得EC=an．
∴AB=2an．
又∵ =n，
∴ 
，
∴BC=2a．
∵MN∥BE，MN⊥MC，
∴∠EFC=∠HMC=90°，
∴∠FCB+∠FBC=90°．
∵∠MBC=90°，
∴∠BMC+∠FCB=90°，
∴∠BMC=∠FBC．
∵∠MBC=∠BCE=90°，
∴△MBC∽△BCE，
∴ 
，
∴ 
，
∴n=4．
【解析】（1）如图1，易证△BMF≌△ECF，则有BM=EC，然后根据E为CD的中点及AB=DC就可得到AM=EC；（2）如图2，设MB=a，易证△ECF∽△BMF，根据相似三角形的性质可得EC=2a，由此可得AB=4a，AM=3a，BC=AD=2a．易证△AMN∽△BCM，根据相似三角形的性质即可得到AN= a，从而可得ND=AD﹣AN= a，就可求出 的值；（3）如图3，设MB=a，依据相似三角形的性质可得BC=2a，CE=na．由MN∥BE，MN⊥MC可得∠EFC=∠HMC=90°，从而可证到△MBC∽△BCE，然后根据相似三角形的性质即可求出n的值．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等．
