题目内容
【题目】如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE. 
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
【答案】
(1)解:连接CD,
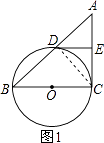
∵BC是⊙O的直径,
∴∠BDC=90°,
即CD⊥AB,
∵AD=DB,OC=5,
∴CD是AB的垂直平分线,
∴AC=BC=2OC=10
(2)证明:连接OD,如图所示,
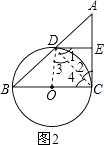
∵∠ADC=90°,E为AC的中点,
∴DE=EC= ![]() AC,
AC,
∴∠1=∠2,
∵OD=OC,
∴∠3=∠4,
∵AC切⊙O于点C,
∴AC⊥OC,
∴∠1+∠3=∠2+∠4=90°,
即DE⊥OD,
∴ED是⊙O的切线.
【解析】(1)连接CD,由直径所对的圆周角为直角可得:∠BDC=90°,即可得:CD⊥AB,然后根据AD=DB,进而可得CD是AB的垂直平分线,进而可得 AC=BC=2OC=10;(2)连接OD,先由直角三角形中线的性质可得DE=EC,然后根据等边对等角可得∠1=∠2,由OD=OC,根据等边对等角可得∠3=∠4,然后根据切线的性质可得∠2+∠4=90°,进而可得:∠1+∠3=90°,进而可得:DE⊥OD,从而可得:ED是⊙O的切线.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如表:
质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全如图的直方图(各组中数据包括左端点不包括右端点). 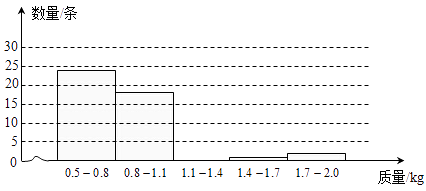
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).