��Ŀ����
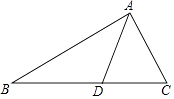
����Ŀ�����ɶ������ض��������֤����������������в�ͬ�����еġ������������С������У�����ϲ�ط��֣�������ȫ�ȵ�ֱ����������ͼ1��ͼ2�ڷ�ʱ���������á����������֤����������С������ͼ1֤�����ɶ����Ĺ��̣�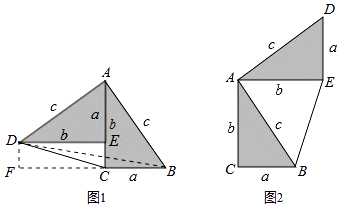
������ȫ�ȵ�ֱ�������ΰ�ͼ1��ʾ�ڷţ����С�DAB=90�㣬��֤��a2+b2=c2 ��
֤��������DB������D��BC���ϵĸ�DF����DF=EC=b��a��
��S�ı���ADCB=S��ACD+S��ABC= ![]() b2+
b2+ ![]() ab��
ab��
�֡�S�ı���ADCB=S��ADB+S��DCB= ![]() c2+
c2+ ![]() a��b��a��
a��b��a��
�� ![]() b2+
b2+ ![]() ab=
ab= ![]() c2+
c2+ ![]() a��b��a��
a��b��a��
��a2+b2=c2
���������֤��������ͼ2��������֤����
������ȫ�ȵ�ֱ�������ΰ�ͼ2��ʾ�ڷţ����С�DAB=90�㣮
��֤��a2+b2=c2
֤��������
��S�����ACBED=
�֡�S�����ACBED=
��
��a2+b2=c2 ��
���𰸡�[ "BD������B��DE���ϵĸ�BF����BF=b��a", "S��ACB+S��ABE+S��ADE= ![]() ab+
ab+ ![]() b2+
b2+ ![]() ab", "S��ACB+S��ABD+S��BDE=
ab", "S��ACB+S��ABD+S��BDE= ![]() ab+
ab+ ![]() c2+
c2+ ![]() a��b��a��", "
a��b��a��", "![]() ab+
ab+ ![]() b2+
b2+ ![]() ab=
ab= ![]() ab+
ab+ ![]() c2+
c2+ ![]() ��������֤��������BD������B��DE���ϵĸ�BF����BF=b��a��
��������֤��������BD������B��DE���ϵĸ�BF����BF=b��a��
��S�����ACBED=S��ACB+S��ABE+S��ADE= ![]() ab+
ab+ ![]() b2+
b2+ ![]() ab��
ab��
�֡�S�����ACBED=S��ACB+S��ABD+S��BDE= ![]() ab+
ab+ ![]() c2+
c2+ ![]() a��b��a����
a��b��a����
�� ![]() ab+
ab+ ![]() b2+
b2+ ![]() ab=
ab= ![]() ab+
ab+ ![]() c2+
c2+ ![]() a��b��a����
a��b��a����
��a2+b2=c2 �� 

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�����Ŀ��Ϊ�˹��������г�Ʒ�㣨����������0.5kg�����ϣ���ͬ�������������ȴ������в���50����Ʒ�㣬�Ƶ����ǵ����������
����/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
����/�� | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
Ȼ�����ϼǺ��ٷŻ�ˮ���У��������ֲ�����100����Ʒ�㣬��������2�����мǺţ�
��1������ݱ������ݲ�ȫ��ͼ��ֱ��ͼ�����������ݰ�����˵㲻�����Ҷ˵㣩�� 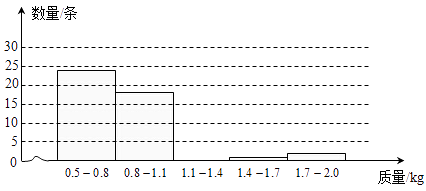
��2������ͼ�����ݷ��飬���ƴ������������һ����Ʒ�㣬������������һ��Ŀ��������
��3������ͼ�����ݷ��飬���������������еȵij�Ʒ�㣬������������һ���ڣ�
��4���������ʵ��ķ������������г�Ʒ�������������ȷ��1kg����