题目内容
【题目】如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF//BC交DC的延长线于点F,连接AF并延长BC的延长线于点G 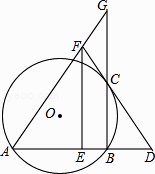
(1)求证:FC=FG;
(2)若BC=4,CG=6,求AB的长.
【答案】
(1)证明:∵EF//BC,BC⊥AB,
∴EF⊥AB,
∵E为AD中点,
∴AF=DF,
∴∠A=∠D,
∵BC⊥AD,
∴∠ABC=∠CBD=90°,
∴∠A+∠G=∠D+∠DCB=90°,
∵∠FCG=∠BCD,
∴∠G=∠FCG,
∴FC=FG;
(2)解:连接AC,
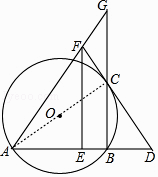
∵∠ABC=90°,
∴∠ACB+∠CAB=90°,
∵DF为切线,
∴∠ACD=90°,
∴∠ACB+∠DCB=90°,
∴∠CAB=∠BCD,
∵∠G=∠FCG=∠BCD,
∴∠CAB=∠G,
∵∠ABC=∠ABG,
∴△ABC∽△GBA,
∴ ![]() =
= ![]() ,
,
∴AB2=BCGB=4×(4+6)=40,
∴AB= ![]() =2
=2 ![]()
【解析】(1)求出EF⊥AB,根据线段垂直平分线性质得出AF=DF,求出∠A=∠D,根据三角形内角和定理求出∠G=∠FCG,即可得出答案;(2)连接AC,求出∠G=∠CAD,根据相似三角形的判定得出△ABC∽△GBA,得出比例式,打扰求出即可.
【考点精析】利用勾股定理的概念和切线的性质定理对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


















