题目内容
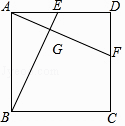
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.

(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接ME.试判断ME与BC是否垂直,并说明理由.
【答案】(1)见解析;(2)ME⊥BC.
【解析】
试题分析:(1)首先根据∠BAC=90°,AF⊥AE可得∠1=∠2,然后根据FC⊥BC,得出∠B=∠FCA=45°,根据条件利用ASA证明△ABE≌△ACF,继而可得BE=CF;
(2)过点E作EH⊥AB于H,求出△BEH是等腰直角三角形,然后求出HE=BH,再根据角平分线上的点到角的两边距离相等可得DE=HE,然后求出HE=HM,从而得到△HEM是等腰直角三角形,再根据等腰直角三角形的性质求解即可.
解:(1)∵∠BAC=90°,AF⊥AE,
∴∠1+∠EAC=90°,∠2+∠EAC=90°
∴∠1=∠2,
又∵AB=AC,
∴∠B=∠ACB=45°,
∵FC⊥BC,
∴∠FCA=90°﹣∠ACB=90°﹣45°=45°,
∴∠B=∠FCA,
在△ABE和△ACF中,
 ,
,
∴△ABE≌△ACF(ASA),
∴BE=CF;
(2)如图,过点E作EH⊥AB于H,则△BEH是等腰直角三角形,
∴HE=BH,∠BEH=45°,
∵AE平分∠BAD,AD⊥BC,
∴DE=HE,
∴DE=BH=HE,
∵BM=2DE,
∴HE=HM,
∴△HEM是等腰直角三角形,
∴∠MEH=45°,
∴∠BEM=45°+45°=90°,
∴ME⊥BC.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目