Question

【题目】）如图，在正方形ABCD中，AB=4cm，动点M从A出发，以1cm/s的速度沿折线AB﹣BC运动，同时动点N从A出发，以2cm/s的速度沿折线AD﹣DC﹣CB运动，M，N第一次相遇时同时停止运动．设△AMN的面积为y，运动时间为x，则下列图象中能大致反映y与x的函数关系的是（ ）

A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：设M，N第一次相遇时间为xs，
由题意得：2x+x=16，
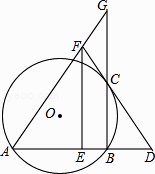
解得x= ；
根据题意：
当点N在AD边，或在DC边上运动时，点M均在AB边上运动；
当点N在BC边上运动时，点M、N均在BC边上运动，直到相遇停止；
此时MN=4﹣（2x﹣8）﹣（x﹣4）=﹣3x+16
∴y= ，
故选C．
【考点精析】解答此题的关键在于理解函数的图象的相关知识，掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．