题目内容
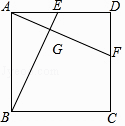
【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

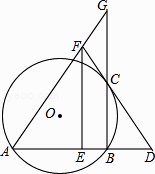
(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

【答案】(1)①α=12°,β=6°;②α=18°,β=9°,③α=2β,理由见解析;(2)α=2β-180°
【解析】试题分析:(1)①先根据角的和与差求α的值,根据等腰三角形的两个底角相等及顶角为30°得:∠ADE=∠AED=75°,同理可得:∠ACB=∠B=69°,根据外角性质列式:75°+β=69°+12°,可得β的度数;
②同理可求得:α=54°﹣36°=18°,β=9°;
③设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,分别求出∠ADE和∠B,根据∠ADC=∠B+α列式,可得结论;
(2)α=2β﹣180°,理由是:如图(2),设∠E=x°,则∠DAC=2x°,根据∠ADC=∠B+∠BAD,列式可得结论.
解:(1)①∵∠DAE=30°,
∴∠ADE+∠AED=150°,
∴∠ADE=∠AED=75°,
∵∠BAC=42°,
∴α=42°﹣30°=12°,
∴∠ACB=∠B=![]() =69°,
=69°,
∵∠ADC=∠B+α,
∴75°+β=69°+12°,
β=6°;
故答案为:12°,6°;
②∵∠DAE=36°,
∴∠ADE+∠AED=144°,
∴∠ADE=∠AED=72°,
∵∠BAC=54°,
∴α=54°﹣36°=18°,
∴∠ACB=∠B=![]() =63°,
=63°,
∵∠ADC=∠B+α,
∴72°+β=63°+18°,
β=9°;
故答案为:18°,9°;
③α=2β,理由是:
如图(1),设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,
∵∠ACB=∠ABC,
∴∠ACB=![]() ,
,
∵∠ADE=∠AED,
∴∠AED=![]() ,
,
∴β+∠ADE=α+∠ABC,
β+![]() =α+
=α+![]() ,
,
∴α=2β;
(2)α=2β﹣180°,理由是:
如图(2),设∠E=x°,则∠DAC=2x°,
∴∠BAC=∠BAD+∠DAC=α+2x°,
∴∠B=∠ACB=![]() ,
,
∵∠ADC=∠B+∠BAD,
∴β﹣x°=![]() +α,
+α,
∴α=2β﹣180°.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 |
|
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 |
|
积与和的商 | (﹣2)÷2=﹣1 |
|
|
(2)请用你发现的规律求出图④中的数x.