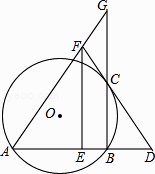
题目内容
【题目】已知如图,圆P经过点A(﹣4,0),点B(6,0),交y轴于点C,∠ACB=45°,连结AP、BP. 
(1)求圆P的半径;
(2)求OC长;
(3)在圆P上是否存在点D,使△BCD的面积等于△ABC的面积?若存在求出点D坐标;若不存在说明理由.
【答案】
(1)解:∵A(﹣4,0),B(6,0)
∴AB=10,
∵∠ACB=45°,
∴∠APB=90°,
∴△PAB为等腰直角三角形,且PA=PB,
∴PA2+PB2=AB2,
解得PA=PB= ![]() ,
,
∴圆P的半径为 ![]()
(2)解:作PM⊥x轴于M,PN⊥y轴于N,连接PC,

∵△PAB为等腰直角三角形,
∴PM=AM=BM ![]() AB=5,
AB=5,
∴OM=AM﹣AO=1,
∴ON=PM=5,PN=OM=1,
在Rt△PNC中有:CN= ![]() =
= ![]() =7,
=7,
∴OC=ON+NC=5+7=12,
∴OC=12
(3)解:∵S△BCD=S△ABC,D为圆P上一点,
①当D与A重合时,仍满足条件,
∴D1(﹣4,0),
②当D与A不重合时,过A作BC的平行线,
与圆P的交点,即为所求的点D,
∵AD∥BC
∴S△BCD=S△ABC(等底等高),
作AG⊥BC于G,作DH⊥BC于H,DQ⊥x轴于Q,

∵cos∠ABC= ![]() ,sin∠ABC=
,sin∠ABC= ![]() ,
,
∴AG=ABcos∠ABC= ![]() ,
,
∵DH=AG=ABsin∠ABC= ![]() ,
,
∵∠DBC=∠DAC=∠ACB=45°,
∴BH=DH= ![]() ,
,
∴AD=GH=BH﹣BG= ![]() ,
,
∴DQ=ADsin∠DAQ=ADsin∠ABC=4,
AQ=ADcos∠DAQ=ADcos∠ABC=2,
∴OQ=OA+AQ=6,
∴D2(﹣6,4)
综上:D点的坐标为(﹣4,0)或(﹣6,4).
【解析】(1)由∠APB=2∠ACB=90°,AB=10,△PAB为等腰直角三角形,即可求得圆P的半径;(2)作PN⊥OC,PM⊥x轴,则ON=PM= ![]() AB=5,再根据勾股定理求出CN的长度,则OC=ON+NC;(3)分两种情况,①当D与A重合时,易得D(﹣4,0),②当D与A重合时,根据等底等高的性质,过A作BC的平行线,与圆P的交点即为所求的点D.
AB=5,再根据勾股定理求出CN的长度,则OC=ON+NC;(3)分两种情况,①当D与A重合时,易得D(﹣4,0),②当D与A重合时,根据等底等高的性质,过A作BC的平行线,与圆P的交点即为所求的点D.

【题目】2018年6月上海语文把小学教材中“外婆”改成“姥姥一事,引起社会的广泛关注和讨论,明德集团某校文学社就此召开了一次研讨会,为了传承中国传统文化,并组织了一次全体学生“汉字听写”大赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果作为样本进行整理,绘制成如下的统计图表:

组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)求统计表中的m,n,并补全条形统计图;
(2)扇形统计图中“C组“所对应的圆心角的度数是多少;
(3)已知该校共有600名学生,如果听写正确的字的个数不少于24个定为合格,请你估计该校本次听写比赛合格的学生人数.
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.