Question

【题目】在Rt△ABC中，∠ACB=90°，AC=3，BC=4．以点C为圆心，r为半径的圆与边AB（边AB为线段）仅有一个公共点，则r的值为（　　）

A.r≥B.r=3或r=4C.≤r≤4 D.r=或3＜r≤4

Answer 1

【答案】D

【解析】

此题注意两种情况：（1）圆与AB相切时；（2）点A在圆内部，点B在圆上或圆外时．根据勾股定理以及直角三角形的面积计算出其斜边上的高，再根据位置关系与数量之间的联系进行求解．

如图，根据勾股定理求得AB=5．

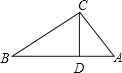
∵BC＞AC，
∴以C为圆心，r为半径所作的圆与斜边AB只有一个公共点．
分两种情况：
（1）圆与AB相切时，即r=CD=3×4÷5=；
（2）点A在圆内部，点B在圆上或圆外时，此时AC＜r≤BC，即3＜r≤4．
∴r＝或3＜r≤4．
故选：D．