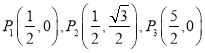题目内容
【题目】综合与探究
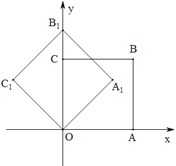
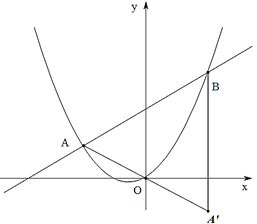
如图,抛物线![]() 的图象经过坐标原点O,且与
的图象经过坐标原点O,且与![]() 轴的另一交点为(
轴的另一交点为(![]() ,0).
,0).
(1)求抛物线的解析式;
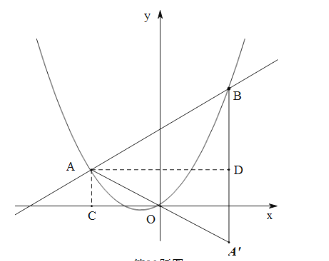
(2)若直线![]() 与抛物线相交于点A和点B(点A在第二象限),设点A′是点A关于原点O的对称点,连接A′B,试判断ΔAA′B的形状,并说明理由;
与抛物线相交于点A和点B(点A在第二象限),设点A′是点A关于原点O的对称点,连接A′B,试判断ΔAA′B的形状,并说明理由;
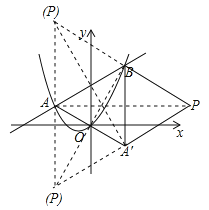
(3)在问题(2)的基础上,探究:平面内是否存在点P,使得以点A,B,A′,P为顶点的四边形是菱形?若存在直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)ΔAA′B是等边三角形;(3)存在,
;(2)ΔAA′B是等边三角形;(3)存在,![]() ,
,![]() ,
,![]()
【解析】
(1)根据点的坐标,利用待定系数法即可求出抛物线F的解析式;
(2)先求出点A、B的坐标,利用对称性求出点A′的坐标,利用两点间的距离公式(勾股定理)可求出AB、AA′、A′B的值,由三者相等即可得出△AA′B为等边三角形;
(3)根据等边三角形的性质结合菱形的性质,可得出存在符合题意得点P,设点P的坐标为(x,y),分三种情况考虑:①当A′B为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;②当AB为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;③当AA′为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标.综上即可得出结论.
解:(1)∵抛物线y=x2+bx+c的图象经过点(0,0)和(![]() ,0),
,0),
∴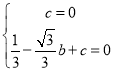 ,解得:
,解得: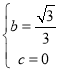 ;
;
∴![]() .
.
(2)ΔAA′B是等边三角形;
∵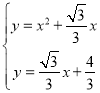 ,
,
解得: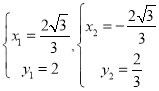 ,
,
∴A(![]() ),B(
),B(![]() ),
),
过点A分别作AC⊥![]() 轴,AD⊥A′B,垂足分别为C,D,
轴,AD⊥A′B,垂足分别为C,D,
∴AC=![]() ,OC=
,OC=![]() ,
,
在RtΔAOC中
OA=![]() ,
,
∵点A′与点A关于原点对称,
∴A′(![]() ),AA′=
),AA′=![]() ,
,
∵B(![]() ),
),
∴A′B=2-(-![]() )=
)=![]() ,
,
又∵A(![]() ),B(
),B(![]() ),
),
∴AD=![]() ,BD=
,BD=![]() ,
,
在RtΔABD中
AB=![]() ,
,
∴AA′=A′B=AB,
∴ΔAA′B是等边三角形;
(3)存在符合题意的点P,且以点A、B、A′、P为顶点的菱形分三种情况;
设点P的坐标为:(x,y).
①当A′B为对角线时,有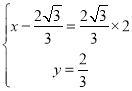 ,
,
解得: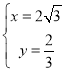 ,
,
∴点P为:![]() ;
;
②当AB为对角线时,有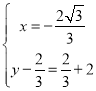 ,
,
解得: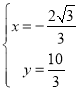 ,
,
∴点P为:![]() ;
;
③当AA′为对角线时,有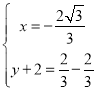 ,
,
解得: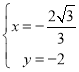 ,
,
∴点P为:![]() ;
;
综合上述,![]() ,
,![]() ,
,![]() .
.

 名校课堂系列答案
名校课堂系列答案