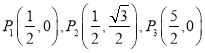Question

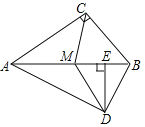
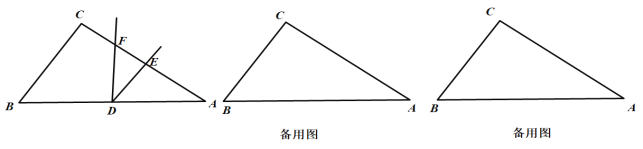
【题目】已知：如图，在中，，，，是斜边的中点，以为顶点，作，的两边交边于点、（点不与点重合）

（1）当时，求的长度；

（2）当绕点转动时，设，，求关于的函数解析式，并写出的取值范围.

（3）联结，是否存在点，使△与△相似？若存在，请求出此时的长度；若不存在，请说明理由.

Answer 1

【答案】（1） （2） （3）或

【解析】

（1）分∠DFE=90°和∠DEF=90°两种情况，根据直角三角形的性质和相似三角形的性质解答；

（2）连接CD，证明△CDE∽△AFD，根据相似三角形的对应边成比例计算即可；

（3）分△BFD∽△AED和△BFD∽△DAE两种情况讨论，根据相似三角形的判定和性质解答．

（1）∵，，，

∴BC=3.

∵，

∴∠ADF=∠ACB=90°，

∵∠A=∠A,

∴△ADF∽△ACB，

∴AD:AC=AF:AB，

∴AF=，

则CF=，

∴CF的长为；

(2)连接CD,

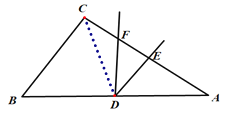
∵D是斜边AB上的中点，

∴AD=DB=CD=2.5，

∴∠DCA=∠DAC，

又∵∠FDE=∠A，

∴∠CDE=∠AFD，

又∵∠DCA=∠DAC，

∴△CDE∽△AFD，

∴CD:AF=CE:AD,即2.5:(4-x)=y:2.5，

∴；

(3)如图，

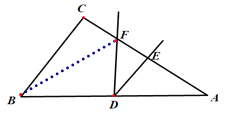
①当△BFD∽△ADE，

则∠FBD=∠A,

∴FB=FA，

则BF2=CF2+BC2，

∴(4-CF)2=CF2+9

解得CF=；

②当△BFD∽△DAE，

则∠BFD=∠A，

∴△BFD∽△BAF，

BF:AB=BD:BF，

∴BF2=，

∴CF==.

∴当CF=或时，△与△相似.